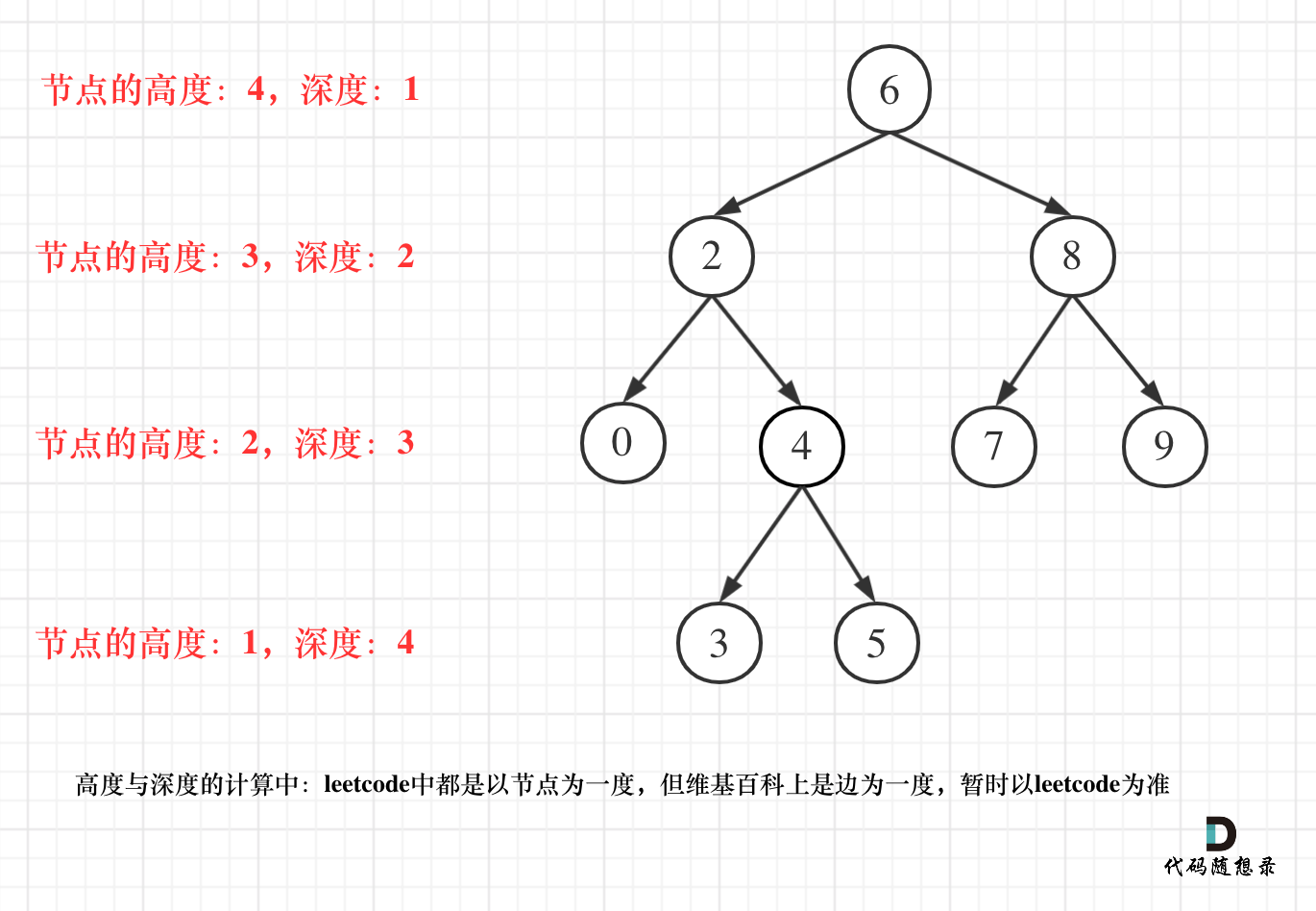
二叉树
二叉树分类
二叉树
完全二叉树
- 定义:除了最底层的节点可能没有填满,其余每层的节点数都达到最大值,并且最下层的节点都集中在该层最左边的若干位置。若最底层为第h层,则该层包含1~2^(h-1)个节点。
平衡二叉树
- 定义:一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
二叉搜索树
一般定义(有些题目有变化,具体因题目而定):
- 结点左子树中所含节点的值 小于等于 当前节点的值
结点右子树中所含节点的值 大于等于 当前节点的值
左子树和右子树都是二叉搜索树
- 结点左子树中所含节点的值 小于等于 当前节点的值
平衡二叉搜索树
References:
遍历
深度优先遍历
前序遍历(递归法,迭代法)
/** * @param {TreeNode} root * @return {number[]} */ var preorderTraversal = function(root) { /* 迭代法实现 */ let result = []; let stack = []; if (root === null) { return result; } stack.push(root); // 注意入栈顺序是先右孩子再左孩子,这样出栈就是根->左->右 while (stack.length) { let node = stack.pop(); result.push(node.val); if (node.right) { stack.push(node.right); } if (node.left) { stack.push(node.left); } } return result; };中序遍历(递归法,迭代法)
/** * @param {TreeNode} root * @return {number[]} */ var inorderTraversal = function(root) { let stack = []; let inorder = []; while (root !== null || stack.length) { if (root !== null) { // 遍历左子树,压栈 stack.push(root); root = root.left; } else { // 中节点出栈 let node = stack.pop(); inorder.push(node.val); // 遍历右子树,压栈 root = root.right; } } return inorder; };后序遍历(递归法,迭代法)
/** * @param {TreeNode} root * @return {number[]} */ var postorderTraversal = function(root) { let postOrder = []; let stack = []; if (root === null) { return postOrder; } stack.push(root); while (stack.length) { let node = stack.pop(); postOrder.push(node.val); // 只改变了前序遍历左右子树的入栈顺序(中--》出栈--》左---》右)---出栈顺序变成了中右左 if (node.left) { stack.push(node.left); } if (node.right) { stack.push(node.right); } } // 这里颠倒数组顺序就变成了左右中 postOrder.reverse(); return postOrder; };
广度优先遍历
层序遍历(队列实现)
/** * @param {TreeNode} root * @return {number[][]} */ var levelOrder = function(root) { let result = []; if (root === null) { return result; } let queue = []; queue.push(root); while (queue.length) { let size = queue.length; // 队列长度 let resPerLevel = []; // 每一层遍历的结果 while (size--) { let node = queue.shift(); resPerLevel.push(node.val); if (node.left) { queue.push(node.left); } if (node.right) { queue.push(node.right); } } result.push(resPerLevel); } return result; };前中后统一的迭代遍历模板
/** * @param {TreeNode} root * @return {number[]} */ var orderTraversal = function(root) { let stack = []; let preOrder = []; // inorder, postorder if (root === null) { return preOrder; } stack.push(root); while (stack.length) { let node = stack.pop(); if (node !== null) { // 这里体现遍历顺序---入栈的顺序和遍历顺序相反(出栈) if (node.right) { stack.push(node.right); // 右 } if (node.left) { stack.push(node.left); //左 } stack.push(node); // 中 stack.push(null); // 标记要放入结果集的节点 } else { node = stack.pop(); preOrder.push(node.val); } } return preOrder; };
创建二叉树
101 对称二叉树
给你一个二叉树的根节点 root , 检查它是否轴对称。


思路:分别比较外侧节点和内侧节点。
(1)递归
/**
* @param {TreeNode} root
* @return {boolean}
*/
var isSymmetric = function(root) {
if (root === null) {
return false;
}
return compare(root.left, root.right);
};
function compare(leftRoot, rightRoot) {
// 后序遍历
// 排除空节点的情况---(终止条件)
if (leftRoot === null && rightRoot !== null) {
return false;
} else if (leftRoot !== null && rightRoot === null) {
return false;
} else if (leftRoot === null && rightRoot === null) {
return true;
} else if (leftRoot.val !== rightRoot.val) {
return false;
}
// 此时两个节点的值相同---(单层递归的逻辑)
let outside = compare(leftRoot.left, rightRoot.right); // 比较外侧的节点
let inside = compare(leftRoot.right, rightRoot.left); // 比较内侧的节点
let isSame = outside && inside;
return isSame;
}(2)迭代(栈或队列都可以,栈是先比较内侧后比较外侧,队列相反)
/**
* @param {TreeNode} root
* @return {boolean}
*/
var isSymmetric = function(root) {
if (root === null) {
return false;
}
let stack = [];
// 根节点的左右子节点入队
stack.push(root.left);
stack.push(root.right);
// 迭代法---层
while (stack.length) {
// 取出栈顶的两个节点
let leftNode = stack.pop();
let rightNode = stack.pop();
// 如果这两个节点都为null,说明这一侧的节点都是对称的
if (leftNode === null && rightNode === null) {
continue;
}
// 如果这两个节点其中一个为null而另一个不为null或者这两个节点的值不相等,则不对称
if ((leftNode === null && rightNode !== null) || (leftNode !== null && rightNode === null) || (leftNode.val !== rightNode.val)) {
return false;
}
// 外侧的节点
stack.push(leftNode.left);
stack.push(rightNode.right);
// 内侧的节点
stack.push(leftNode.right);
stack.push(rightNode.left);
}
return true;
};104 二叉树的最大深度
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7返回它的最大深度 3 。
深度和高度的区别?
二叉树节点的深度:从根节点到该节点的最长简单路径边的条数。
二叉树节点的高度:从该节点到叶子结点的最长简单路径边的条数。
但LeetCode中的深度和高度是按照
节点来计算的。
思路:递归(前序或后序),迭代(层序)
(1)递归
/**
* @param {TreeNode} root
* @return {number}
*/
var maxDepth = function(root) {
let result = 0;
if (root === null) {
return result;
}
// 前序遍历,depth从1开始
const getMaxDepth = (root, depth) => {
result = depth > result ? depth : result;
// 到达叶子结点
if (root.left === null && root.right === null) {
return ;
}
if (root.left) {
getMaxDepth(root.left, depth + 1);
}
if (root.right) {
getMaxDepth(root.right, depth + 1);
}
return ;
}
getMaxDepth(root, 1);
return result;
};
/**
* @param {TreeNode} root
* @return {number}
*/
var maxDepth = function(root) {
let result = 0;
if (root === null) {
return result;
}
// 后序遍历
const getMaxDepth = (root) => {
if (root === null) {
return 0;
}
let leftDepth = getMaxDepth(root.left);
let rightDepth = getMaxDepth(root.right);
let depth = Math.max(leftDepth, rightDepth) + 1; // 从叶子结点往上加
return depth;
}
result = getMaxDepth(root, 1);
return result;
};(2)迭代
/**
* @param {TreeNode} root
* @return {number}
*/
var maxDepth = function(root) {
let result = 0;
if (root === null) {
return result;
}
let queue = [];
queue.push(root)
// 层序遍历
// 进入每一层
while (queue.length) {
let size = queue.length;
result++;
while (size--) {
let node = queue.shift();
if (node.left) {
queue.push(node.left);
}
if (node.right) {
queue.push(node.right);
}
}
}
return result;
};559 N叉树的最大深度
给定一个 N 叉树,找到其最大深度。
最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。
N 叉树输入按层序遍历序列化表示,每组子节点由空值分隔(请参见示例)。
示例 1:

输入:root = [1,null,3,2,4,null,5,6]
输出:3示例 2:

输入:root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出:5提示:
树的深度不会超过 1000 。
树的节点数目位于 [0, 104] 之间。
思路:跟二叉树的区别就是子节点的地方,N叉树的子节点通过root.children访问,children是一个节点数组,里面都是root的子节点
(1)递归
/**
* // Definition for a Node.
* function Node(val,children) {
* this.val = val;
* this.children = children;
* };
*/
/**
* @param {Node|null} root
* @return {number}
*/
var maxDepth = function(root) {
let result = 0;
if (root === null) {
return result;
}
// 前序遍历
const getMaxDepth = (node, depth) => {
if (node.left === null && node.right === null) {
return ;
}
result = depth > result ? depth : result;
// 循环遍历多个子节点
for (let i = 0; i < node.children.length; i++) {
if (node.children[i]) {
depth++;
getMaxDepth(node.children[i], depth);
depth--;
}
}
}
getMaxDepth(root, 1);
return result;
};/**
* // Definition for a Node.
* function Node(val,children) {
* this.val = val;
* this.children = children;
* };
*/
/**
* @param {Node|null} root
* @return {number}
*/
var maxDepth = function(root) {
let result = 0;
if (root === null) {
return result;
}
// 后序遍历
const getMaxDepth = (node) => {
if (node === null) {
return 0;
}
let depth = 0;
// 循环遍历多个子节点
for (let i = 0; i < node.children.length; i++) {
depth = Math.max(depth, getMaxDepth(node.children[i]));
}
return depth + 1;
}
result = getMaxDepth(root, 1);
return result;
};(2)迭代
/**
* // Definition for a Node.
* function Node(val,children) {
* this.val = val;
* this.children = children;
* };
*/
/**
* @param {Node|null} root
* @return {number}
*/
var maxDepth = function(root) {
let result = 0;
if (root === null) {
return result;
}
// 层序遍历
let queue = [];
queue.push(root);
while (queue.length) {
let size = queue.length;
result++;
while (size--) {
let node = queue.shift();
for (const childNode of node.children) {
if (childNode) {
queue.push(childNode)
}
}
}
}
return result;
};111 二叉树的最小深度
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:叶子节点是指没有子节点的节点。
示例 1:

输入:root = [3,9,20,null,null,15,7]
输出:2示例 2:
输入:root = [2,null,3,null,4,null,5,null,6]
输出:5提示:
- 树中节点数的范围在
[0, 105]内 -1000 <= Node.val <= 1000
最小深度跟最大深度的解法类似,不同的是处理左右孩子不为空的逻辑。
注意:最小深度是从根节点到最近叶子结点的最短路径上的节点数量。
(1)迭代
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number}
*/
var minDepth = function(root) {
let result = 0;
// 后序遍历
const getMinDepth = (node) => {
if (node === null) {
return 0;
}
let leftDepth = getMinDepth(node.left); // 左
let rightDepth = getMinDepth(node.right); // 右
// 中
// 左节点为空,右节点不为空
if (node.left === null && node.right !== null) {
return 1 + rightDepth;
}
// 左节点不为空,右节点为空
if (node.left !== null && node.right === null) {
return 1 + leftDepth;
}
// 左右节点都为空或者都不为空
let minDepth = Math.min(leftDepth, rightDepth) + 1;
return minDepth;
}
result = getMinDepth(root);
return result;
};(2)迭代
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number}
*/
var minDepth = function(root) {
let depth = 0;
if (root === null) {
return depth;
}
let queue = [];
queue.push(root);
// 层序遍历
while (queue.length) {
let size = queue.length;
depth++;
while (size--) {
let node = queue.shift();
if (node.left) {
queue.push(node.left);
}
if (node.right) {
queue.push(node.right);
}
if (node.left === null && node.right === null) { // 当这一层的某个节点左节点和右节点都为空时,说明是最低层了。
return depth;
}
}
}
return depth;
};222 完全二叉树的节点个数
给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。
完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2h 个节点。

示例 1:
输入:root = [1,2,3,4,5,6]
输出:6
示例 2:
输入:root = []
输出:0
示例 3:
输入:root = [1]
输出:1
提示:
树中节点的数目范围是[0, 5 * 104]
0 <= Node.val <= 5 * 104
题目数据保证输入的树是 完全二叉树
进阶:遍历树来统计节点是一种时间复杂度为 O(n) 的简单解决方案。你可以设计一个更快的算法吗?
思路:
- 二叉树的后序遍历
- 二叉树的层序遍历
- 完全二叉树的性质(子树是满二叉树)
(1)后序遍历
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number}
*/
var countNodes = function(root) {
let result = 0;
// 后序遍历
const getNodesCount = (node) => {
if (node === null) {
return 0;
}
let leftNodesCount = getNodesCount(node.left); // 左
let rightNodesCount = getNodesCount(node.right); // 右
let count = leftNodesCount + rightNodesCount + 1; // 中(+1 => 节点数=1+左子树节点数+右子树节点数)
return count;
}
result = getNodesCount(root);
return result;
};(2)层序遍历
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number}
*/
var countNodes = function(root) {
let nodesNum = 0;
if (root == null) {
return nodesNum;
}
// 层序遍历
let queue = [root];
while (queue.length) {
let size = queue.length;
nodesNum += size; // 加上每一层的节点数
while (size--) {
let node = queue.shift();
if (node.left) {
queue.push(node.left);
}
if (node.right) {
queue.push(node.right);
}
}
}
return nodesNum;
};(3)完全二叉树的性质
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number}
*/
var countNodes = function(root) {
// 利用完全二叉树的性质
if (root === null) {
return 0;
}
let leftHight = 0;
let rightHight = 0;
let left = root.left;
let right = root.right;
while (left) {
left = left.left;
leftHight++;
}
while (right) {
right = right.right;
rightHight++;
}
// 递归到满二叉树为止
if (rightHight === leftHight) {
// 细节:leftHight + 1
return Math.pow(2, leftHight + 1) - 1;
}
let leftNodesNum = countNodes(root.left);
let rightNodesNum = countNodes(root.right);
return leftNodesNum + rightNodesNum + 1;
};110 平衡二叉树
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
示例 1:

输入:root = [3,9,20,null,null,15,7]
输出:true
示例 2:
输入:root = [1,2,2,3,3,null,null,4,4]
输出:false
示例 3:
输入:root = []
输出:true
提示:
树中的节点数在范围 [0, 5000] 内
-10^4 <= Node.val <= 10^4
思路:
- 后序遍历-递归,求高度,如果不满足条件就返回-1,表示不是平衡二叉树。
- 层序遍历,每个节点都计算左右子树的高度,然后判断是否满足平衡二叉树条件。
(1)后序遍历-递归
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {boolean}
*/
var isBalanced = function(root) {
let result = true;
if (root === null) {
return result;
}
// 后序遍历,-1表示不是平衡二叉树
const getHeight = (node) => {
if (node === null) {
return 0;
}
let leftHeight = getHeight(node.left);
// 当不满足平衡二叉树条件时就退出
if (leftHeight === -1) {
return -1;
}
let rightHeight = getHeight(node.right);
if (rightHeight === -1) {
return -1;
}
let height = 0;
if (Math.abs(leftHeight - rightHeight) > 1) {
height = -1;
} else {
height = Math.max(leftHeight, rightHeight) + 1;
}
return height;
}
if (getHeight(root) === -1) {
result = false;
}
return result;
};
(2)迭代
/**
* @param {TreeNode} root
* @return {boolean}
*/
var isBalanced = function(root) {
if (root === null) {
return true;
}
let stack = [root];
// 前序遍历
while (stack.length) {
let node = stack.pop();
if (Math.abs(getDepth(node.left) - getDepth(node.right)) > 1) {
return false;
}
if (node.right) {
stack.push(node.right);
}
if (node.left) {
stack.push(node.left);
}
}
return true;
};
// 后序遍历得到传入节点的深度
function getDepth(root) {
let depth = 0;
let result = 0;
let stack = [];
if (root !== null) {
stack.push(root);
}
while (stack.length) {
let node = stack.pop();
if (node !== null) {
stack.push(node); // 中
stack.push(null);
depth++;
if (node.right) {
stack.push(node.right); // 右
}
if (node.left) {
stack.push(node.left); // 左
}
} else {
node = stack.pop();
depth--;
}
result = result > depth ? result : depth;
}
return result;
}
周总结
迭代法什么时候用队列,什么时候用栈?
如果模拟前中后序遍历就用栈,模拟层序遍历就用队列。但是也有其他情况,队列和栈都试试看哪个符合题意。
深度和高度的区别?
- 二叉树节点的深度:从根节点到该节点的最长简单路径边的条数。
- 二叉树节点的高度:从该节点到叶子结点的最长简单路径边的条数。
但LeetCode中的深度和高度是按照
节点来计算的。
404 左叶子之和
给定二叉树的根节点 root ,返回所有左叶子之和。
示例 1:
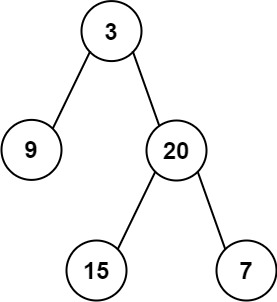
输入: root = [3,9,20,null,null,15,7]
输出: 24
解释: 在这个二叉树中,有两个左叶子,分别是 9 和 15,所以返回 24
示例 2:
输入: root = [1]
输出: 0
提示:
节点数在 [1, 1000] 范围内
-1000 <= Node.val <= 1000
思路:要确定左叶子,需要通过左叶子的父节点来确定
(1)递归
/**
* @param {TreeNode} root
* @return {number}
*/
var sumOfLeftLeaves = function(root) {
if (root === null) {
return 0;
}
let sum = []; // 注意这里用数组来存储左叶子,因为前序会回溯,如果使用number那之前的值就没了
// 前序遍历
const getSum = (node, sum) => {
// 判断是不是左叶子节点
if (node.left && node.left.left === null && node.left.right === null) {
sum.push(node.left.val);
}
// 退出条件
if (node.left === null && node.right === null) {
return ;
}
// 左节点存在才继续递归
if (node.left) {
getSum(node.left, sum);
}
// 右节点存在才继续递归
if (node.right) {
getSum(node.right, sum);
}
}
getSum(root, sum);
if (sum.length) {
return sum.reduce((preValue, curValue) => preValue + curValue);
} else {
return 0;
}
};/**
* @param {TreeNode} root
* @return {number}
*/
var sumOfLeftLeaves = function(root) {
let sum = 0;
// 后序遍历
const getSum = (node) => {
if (node === null) {
return 0;
}
let leftValue = getSum(node.left); // 左子树的左叶子节点之和
let rightValue = getSum(node.right); // 右子树的左叶子节点之和
let midValue = 0;
// 确定左叶子
if (node.left && node.left.left === null && node.left.right === null) {
midValue = node.left.val;
}
let sum = midValue + leftValue + rightValue;
return sum;
}
sum = getSum(root);
return sum;
};(2)迭代
/**
* @param {TreeNode} root
* @return {number}
*/
var sumOfLeftLeaves = function(root) {
let sum = 0;
if (root === null) {
return sum;
}
// 迭代-前序遍历(统一遍历模板)
let stack = [root];
while (stack.length) {
let node = stack.pop();
if (node !== null) {
if (node.right) {
stack.push(node.right);
}
if (node.left) {
stack.push(node.left);
}
stack.push(node);
stack.push(null);
} else {
node = stack.pop();
// 确定是左叶子
if (node.left && node.left.left === null && node.left.right === null) {
sum += node.left.val;
}
}
}
return sum;
};513 找树左下角的值
给定一个二叉树的 根节点 root,请找出该二叉树的 最底层 最左边 节点的值。
假设二叉树中至少有一个节点。
示例 1:

输入: root = [2,1,3]
输出: 1
示例 2:

输入: [1,2,3,4,null,5,6,null,null,7]
输出: 7
提示:
二叉树的节点个数的范围是 [1,104]
-2^31 <= Node.val <= 2^31 - 1
- 递归
- 迭代(层序遍历)
要注意代码细节!
(1)递归
/**
* @param {TreeNode} root
* @return {number}
*/
var findBottomLeftValue = function(root) {
let leftValue = null; // 结果设置为nul,值类型不行(细节)
let maxDepth = 0;
// 前序遍历-深度优先
const getBottomLeftValue = (node, curDepth) => {
if (node.left === null && node.right === null) {
if (curDepth > maxDepth) {
maxDepth = curDepth;
leftValue = node.val;
}
return ;
}
if (node.left) {
getBottomLeftValue(node.left, curDepth + 1);
}
if (node.right) {
getBottomLeftValue(node.right, curDepth + 1);
}
}
getBottomLeftValue(root, maxDepth);
if (leftValue === null) {
leftValue = root.val;
}
return leftValue;
};(2)迭代
/**
* @param {TreeNode} root
* @return {number}
*/
var findBottomLeftValue = function(root) {
let leftValue = 0;
// 层序遍历
let queue = [root];
while (queue.length) {
let size = queue.length;
for (let i = 0; i < size; i++) {
let node = queue.shift();
// 取每层第一个节点
if (i === 0) {
leftValue = node.val;
}
if (node.left) {
queue.push(node.left);
}
if (node.right) {
queue.push(node.right);
}
}
}
return leftValue;
};654 最大二叉树
给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:
创建一个根节点,其值为 nums 中的最大值。
递归地在最大值 左边 的 子数组前缀上 构建左子树。
递归地在最大值 右边 的 子数组后缀上 构建右子树。
返回 nums 构建的 最大二叉树 。
示例 1:

输入:nums = [3,2,1,6,0,5]
输出:[6,3,5,null,2,0,null,null,1]
解释:递归调用如下所示:
- [3,2,1,6,0,5] 中的最大值是 6 ,左边部分是 [3,2,1] ,右边部分是 [0,5] 。
- [3,2,1] 中的最大值是 3 ,左边部分是 [] ,右边部分是 [2,1] 。
- 空数组,无子节点。
- [2,1] 中的最大值是 2 ,左边部分是 [] ,右边部分是 [1] 。
- 空数组,无子节点。
- 只有一个元素,所以子节点是一个值为 1 的节点。
- [0,5] 中的最大值是 5 ,左边部分是 [0] ,右边部分是 [] 。
- 只有一个元素,所以子节点是一个值为 0 的节点。
- 空数组,无子节点。
- [3,2,1] 中的最大值是 3 ,左边部分是 [] ,右边部分是 [2,1] 。
示例 2:

输入:nums = [3,2,1]
输出:[3,null,2,null,1]
提示:
1 <= nums.length <= 1000
0 <= nums[i] <= 1000
nums 中的所有整数 互不相同
传递的参数为数组的索引,而不是子数组。
注意代码细节!
/**
* @param {number[]} nums
* @return {TreeNode}
*/
var constructMaximumBinaryTree = function(nums) {
let root = null;
// 前序遍历
const build = (nums, startIndex, endIndex) => {
if (startIndex === endIndex) {
return null;
}
let maxNum = -1; // 细节(题干条件说了nums[i]>=0,初始化为0那if判断就进不去,maxNumIndex就没有更新)
let maxNumIndex = 0;
for (let i = startIndex; i < endIndex; i++) {
if (nums[i] > maxNum) {
maxNum = nums[i];
maxNumIndex = i;
}
}
let node = new TreeNode(maxNum, null, null);
node.left = build(nums, startIndex, maxNumIndex);
node.right = build(nums, maxNumIndex + 1, endIndex);
return node;
}
root = build(nums, 0, nums.length);
return root;
};112 路径总和
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。
叶子节点 是指没有子节点的节点。
示例 1:

输入:root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出:true
解释:等于目标和的根节点到叶节点路径如上图所示。
示例 2:

输入:root = [1,2,3], targetSum = 5
输出:false
解释:树中存在两条根节点到叶子节点的路径:
(1 –> 2): 和为 3
(1 –> 3): 和为 4
不存在 sum = 5 的根节点到叶子节点的路径。
示例 3:
输入:root = [], targetSum = 0
输出:false
解释:由于树是空的,所以不存在根节点到叶子节点的路径。
提示:
树中节点的数目在范围 [0, 5000] 内
-1000 <= Node.val <= 1000
-1000 <= targetSum <= 1000
前序遍历,回溯
/**
* @param {TreeNode} root
* @param {number} targetSum
* @return {boolean}
*/
var hasPathSum = function(root, targetSum) {
if (root === null) {
return false;
}
// 前序遍历--深度递归(自己实现的思路)
const traverse = (node, targetSum, sum) => {
sum += node.val;
if (node && node.left === null && node.right === null) {
if (sum === targetSum) {
return true;
}
return false;
}
if (node.left) {
if (traverse(node.left, targetSum, sum)) {
return true;
}
}
if (node.right) {
if (traverse(node.right, targetSum, sum)) {
return true;
}
}
return false;
}
let result = traverse(root, targetSum, 0);
return result;
};/**
* @param {TreeNode} root
* @param {number} targetSum
* @return {boolean}
*/
var hasPathSum = function(root, count) {
if (root === null) {
return false;
}
// 回溯的逻辑
const traverse = (node, count) => {
if (!node.left && !node.right && count === 0) {
return true;
}
if (!node.left && !node.right) {
return false;
}
if (node.left) {
count -= node.left.val;
if (traverse(node.left, count)) {
return true;
}
count += node.left.val;
}
if (node.right) {
count -= node.right.val;
if (traverse(node.right, count)) {
return true;
}
count += node.right.val;
}
return false;
}
return traverse(root, count - root.val);
};113 路径总和II
给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。
叶子节点 是指没有子节点的节点。
示例 1:

输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出:[[5,4,11,2],[5,8,4,5]]
示例 2:

输入:root = [1,2,3], targetSum = 5
输出:[]
示例 3:
输入:root = [1,2], targetSum = 0
输出:[]
提示:
树中节点总数在范围 [0, 5000] 内
-1000 <= Node.val <= 1000
-1000 <= targetSum <= 1000
记录所有满足条件的路径,回溯的思想。
到叶子结点处判断是否满足条件,满足条件就记录这条路径,然后返回。
/**
* @param {TreeNode} root
* @param {number} targetSum
* @return {number[][]}
*/
var pathSum = function(root, targetSum) {
let result = [];
let path = [];
let sum = 0;
if (root === null) {
return result;
}
path.push(root.val);
sum = root.val;
// 前序-回溯
const traverse = (node, targetSum, sum) => {
if (node.left === null && node.right === null) {
if (sum === targetSum) {
result.push([...path]);
}
return ;
}
if (node.left) {
sum += node.left.val;
path.push(node.left.val);
traverse(node.left, targetSum, sum);
path.pop();
sum -= node.left.val;
}
if (node.right) {
sum += node.right.val;
path.push(node.right.val);
traverse(node.right, targetSum, sum);
sum -= node.right.val;
path.pop();
}
}
traverse(root, targetSum, sum);
return result;
};总结
什么时候递归要返回值,什么时候不用返回?
如果要搜索整棵树,递归函数就不需要返回值;如果只需要找到某条符合条件的路径,就需要返回。
617 合并二叉树
给你两棵二叉树: root1 和 root2 。
想象一下,当你将其中一棵覆盖到另一棵之上时,两棵树上的一些节点将会重叠(而另一些不会)。你需要将这两棵树合并成一棵新二叉树。合并的规则是:如果两个节点重叠,那么将这两个节点的值相加作为合并后节点的新值;否则,不为 null 的节点将直接作为新二叉树的节点。
返回合并后的二叉树。
注意: 合并过程必须从两个树的根节点开始。
示例 1:

输入:root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
输出:[3,4,5,5,4,null,7]
示例 2:
输入:root1 = [1], root2 = [1,2]
输出:[2,2]
提示:
两棵树中的节点数目在范围 [0, 2000] 内
-10^4 <= Node.val <= 10^4
前中后序遍历都可以,前序最好理解。
两棵树,任意一颗的节点为null就用另外一颗的替代。
/**
* @param {TreeNode} root1
* @param {TreeNode} root2
* @return {TreeNode}
*/
var mergeTrees = function(root1, root2) {
// 前序遍历
// tree1的节点为空,这个时候用tree2的节点
if (root1 === null) {
return root2;
}
// tree2的节点为空,这个时候用tree1的节点
if (root2 === null) {
return root1;
}
root1.val += root2.val;
root1.left = mergeTrees(root1.left, root2.left);
root1.right = mergeTrees(root1.right, root2.right);
return root1;
};226 翻转二叉树

两种解法:
深度优先递归(递归,前序遍历位置执行操作)
广度优先递归(层序遍历,借助一个额外的队列存放当前需要交换左右子节点的根节点)
深度优先遍历(前序遍历)
从树的根节点开始,先遍历左子树,然后遍历右子树
/** * Definition for a binary tree node. * function TreeNode(val, left, right) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } */ /** * @param {TreeNode} root * @return {TreeNode} */ var invertTree = function(root) { if (root == null) { return null; } /* 前序遍历位置 */ // 交换根节点的左右子节点 var temp = root.left; root.left = root.right; root.right = temp; // 继续交换左右子树的节点 invertTree(root.left); invertTree(root.right); return root; };广度优先遍历
从根节点开始,沿着树的宽度依次遍历树的每个节点。(层序遍历)
/** * Definition for a binary tree node. * function TreeNode(val, left, right) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } */ /** * @param {TreeNode} root * @return {TreeNode} */ var invertTree = function(root) { if (root == null) { return null; } // 定义一个队列存放当前要交换位置的孩子的根结点 let queue = []; queue.push(root); // 穷举 while(queue.length != 0) { // 从队列中取出当前节点 var currentNode = queue.shift(); // 交换左右节点 var temp = currentNode.left; currentNode.left = currentNode.right; currentNode.right = temp; // 如果当前节点的左子树不为空,放到队列中 if (currentNode.left != null) { queue.push(currentNode.left); } // 如果当前节点的右子树不为空,放到队列中 if (currentNode.right != null) { queue.push(currentNode.right); } } return root; };
116 填充二叉树节点的右侧指针

递归,主要操作在前序遍历位置,借助一个有两个结点作为参数的函数,因为要在每个节点上执行操作,所以会遍历到每个节点。
/**
* // Definition for a Node.
* function Node(val, left, right, next) {
* this.val = val === undefined ? null : val;
* this.left = left === undefined ? null : left;
* this.right = right === undefined ? null : right;
* this.next = next === undefined ? null : next;
* };
*/
/**
* @param {Node} root
* @return {Node}
*/
var connect = function(root) {
if (root === null) return null;
connectTwoNode(root.left, root.right);
return root;
};
function connectTwoNode(Node1, Node2) {
/* 前序遍历位置 */
/* 结束条件 */
if (Node1 == null || Node2 == null) return;
/* 连接传入的两个节点 */
Node1.next = Node2;
/* 连接Node1的子节点 */
connectTwoNode(Node1.left, Node1.right);
/* 连接Node2的子节点 */
connectTwoNode(Node2.left, Node2.right);
/* 连接Node1和Node2的子节点 */
connectTwoNode(Node1.right, Node2.left);
}114 将二叉树展开为链表

递归,后序遍历。
在函数内要对根节点判空,注意函数的主要操作在后序遍历位置,即在左右子树都拉平后。
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {void} Do not return anything, modify root in-place instead.
*/
var flatten = function(root) {
if (root === null) return null;
// 先序遍历, 将左右子树拉平
flatten(root.left);
flatten(root.right);
/* 后序遍历位置,此时左右子树已经拉平 */
// 左子树作为右子树
let left = root.left;
let right = root.right;
root.left = null;
root.right = left;
// 右子树接到左子树后面
let p = root;
// 找到现在右子树的叶子结点
while(p.right != null) {
p = p.right;
}
// 在叶子结点后接上之前的右子树
p.right = right;
};654 构造最大二叉树

思路1:自己递归自己,在前序遍历位置找到最大值和最大值索引,递归参数为新的数组
思路2:分治思想,递归另外的辅助函数,找到最大值和最大值索引,最大值的初始化值比原数组的最小值小,递归参数为数组的新的索引。
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {number[]} nums
* @return {TreeNode}
*/
[1, 3, 5, 2, 6, 8, 10]
/**
* 思路一
* 递归传递的参数是数组
*/
var constructMaximumBinaryTree = function(nums) {
if (nums.length === 0) return null;
/* 前序遍历位置 */
// 确定并创建根节点
let maxNum = Math.max.apply(Math, nums);
let index = nums.indexOf(maxNum);
let root = new TreeNode(maxNum, null, null);
// 递归创建左子树
root.left = constructMaximumBinaryTree(nums.slice(0, index));
// 递归创建右子树
root.right = constructMaximumBinaryTree(nums.slice(index + 1, nums.length));
return root;
};
/**
* 思路二
* 递归传递的参数是数组的索引
*/
var constructMaximumBinaryTree = function (nums) {
let root = construct(nums, 0, nums.length);
return root;
};
/**
nums: 输入的数组
lo: 数组左边界的索引
hi: 数组右边界的索引
*/
const construct = (arr, lo, hi) => {
if (lo === hi) {
return null;
}
// 这里要特别注意测试用例的数组的值的范围
let index = -1;
let maxValue = -2;
// 找到数组中最大值和相应的索引
for (let i = lo; i < hi; ++i) {
if (arr[i] > maxValue) {
maxValue = arr[i];
index = i;
}
}
// 创建根节点
let root = new TreeNode(maxValue);
// 递归构造左子树
root.left = construct(arr, lo, index);
// 递归构造右子树
root.right = construct(arr, index + 1, hi);
return root;
}105 从前序与中序遍历序列构造二叉树

逻辑处理在前序遍历位置,然后分别递归左子树和右子树。首先确定根节点的值和位置(前序遍历的第一个位置),中序遍历根节点的左边是左子树,右边是右子树,前序遍历的左子树和右子树位置由左子树的长度确定。
难点在如何确定前序遍历中左子树的起始位置。
递归的参数是整个树的前序遍历和中序遍历、树的前序遍历起始索引、树的中序遍历索引。
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {number[]} preorder
* @param {number[]} inorder
* @return {TreeNode}
*/
var buildTree = function (preorder, inorder) {
return build(preorder, 0, preorder.length - 1, inorder, 0, inorder.length - 1);
};
/**
* @param {number[]} preorder 前序遍历序列
* @param {number[]} inorder 中序遍历虚列
* @param {number} preStart 前序遍历序列第一个元素的索引
* @param {number} preEnd 前序遍历序列最后一个元素的索引
* @param {number} inStart 中序遍历序列第一个元素的索引
* @param {number} inEnd 中序遍历序列最后一个元素的索引
* @return {TreeNode}
*/
function build(preorder, preStart, preEnd, inorder, inStart, inEnd) {
// 退出条件
if (preStart > preEnd) return null;
// 找到根节点的值
let rootValue = preorder[preStart];
// 找到根节点在中序遍历中的索引
let rootInIndex = inorder.indexOf(rootValue);
// 左子树的长度
let leftSize = rootInIndex - inStart;
// 确定前序遍历中左子树的起始
let preLStart = preStart + 1;
let preLEnd = preStart + leftSize;
// 确定中序遍历中左子树的起始
let inLStart = inStart;
let inLEnd = rootInIndex - 1;
// 确定前序遍历中右子树的起始
let preRStart = preStart + leftSize + 1;
let preREnd = preEnd;
// 确定中序遍历中右子树的起始
let inRStart = rootInIndex + 1;
let inREnd = inEnd;
// 创建根节点
let root = new TreeNode(rootValue);
// 递归左右子树
root.left = build(preorder, preLStart, preLEnd, inorder, inLStart, inLEnd);
root.right = build(preorder, preRStart, preREnd, inorder, inRStart, inREnd);
return root;
}106 从中序与后序遍历序列构造二叉树

逻辑处理在前序遍历位置,同5类似,根据中序遍历和后序遍历的特点确定递归传递的左右子树起始位置的索引。
中序遍历,根结点的左边是左子树,右边是右子树;
后序遍历,根结点在后序遍历序列的末尾。
根据中序遍历确定左子树的长度,然后确定递归时左右子树遍历序列的起始索引。
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {number[]} inorder
* @param {number[]} postorder
* @return {TreeNode}
*/
var buildTree = function(inorder, postorder) {
return build(inorder, postorder, 0, inorder.length - 1, 0, postorder.length - 1);
};
function build(inorder, postorder, inStart, inEnd, postStart, postEnd) {
// 退出条件
if (inStart > inEnd) return null;
// 确定根节点的值
let rootVal = postorder[postEnd];
// 确定根节点的值在中序遍历中的索引
let rootIndex = inorder.indexOf(rootVal);
// 确定左子树的长度
let leftSize = rootIndex - inStart;
// 创建根节点
let root = new TreeNode(rootVal);
// 递归创建左子树和右子树
root.left = build(inorder, postorder, inStart, rootIndex - 1, postStart, postStart + leftSize - 1);
root.right = build(inorder, postorder, rootIndex + 1, inEnd, postStart + leftSize, postEnd - 1);
return root;
}889 根据前序和后序遍历构造二叉树

和105、106的思路一致,不同之处是退出条件。由前序遍历确定的左子树根节点rootLeft的值可能是rootLeft的右节点的值,此时返回一个新的节点。
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {number[]} preorder
* @param {number[]} postorder
* @return {TreeNode}
*/
var constructFromPrePost = function(preorder, postorder) {
return build(preorder, postorder, 0, preorder.length - 1, 0, postorder.length - 1);
};
function build(preorder, postorder, preStart, preEnd, postStart, postEnd) {
// 退出条件
if (preStart > preEnd) return null;
// 左子树根结点的右结点???
if (preStart === preEnd) return new TreeNode(preorder[preStart]);
// 确定根节点的值
let rootVal = preorder[preStart];
// 确定左子树的长度
let leftVal = preorder[preStart + 1];
let leftSize = postorder.indexOf(leftVal) - postStart + 1;
// 创建根节点
let root = new TreeNode(rootVal);
// 递归创建左右子树
root.left = build(preorder, postorder, preStart + 1, preStart + leftSize, postStart, postStart + leftSize - 1);
root.right = build(preorder, postorder, preStart + leftSize + 1, preEnd, postStart + leftSize, postEnd - 1);
return root;
}
652 寻找重复的子树

这道题的逻辑处理代码是在
后序遍历位置。两种解法:
- 记录每棵子树的序列和出现的次数,并记录有重复序列时的根节点。
>/** >* Definition for a binary tree node. >* function TreeNode(val, left, right) { >* this.val = (val===undefined ? 0 : val) >* this.left = (left===undefined ? null : left) >* this.right = (right===undefined ? null : right) >* } >*/ >/** >* @param {TreeNode} root >* @return {TreeNode[]} >*/ >var findDuplicateSubtrees = function(root) { // 记录子树的序列及出现的次数 let subTreeSeqAndTimes = new Map(); // 记录重复的子树根节点 let repNodes = []; const traverse = (root) => { // 退出条件 if (!root) return '#'; // 迭代左右子树 let left = traverse(root.left); let right = traverse(root.right); // 子树序列化 let subTreeSeq = left + "," + right + "," + root.val; // 在子树的序列化map中找有没有相同的序列,有的话将序列出现的次数赋值给freq let freq = subTreeSeqAndTimes.get(subTreeSeq) || 0; // 判断子树序列是否已经存在,多次重复的序列只存一次根节点 if (freq === 1) { repNodes.push(root); } // 给相应的子树序列出现次数加1 subTreeSeqAndTimes.set(subTreeSeq, freq + 1); return subTreeSeq; } traverse(root); return repNodes; >};
236 二叉树的最近公共祖先

- 递归
- 迭代法,求p到root的路径与q到root 的路径的第一个交点
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* @param {TreeNode} root
* @param {TreeNode} p
* @param {TreeNode} q
* @return {TreeNode}
*/
/* 递归 */
var lowestCommonAncestor = function(root, p, q) {
// 2. 确定递归终止条件
if (root === p || root === q || root === null) {
return root;
}
// 1. 确定递归函数返回值和参数
let left = lowestCommonAncestor(root.left, p, q);
let right = lowestCommonAncestor(root.right, p, q);
// 3. 确定单层逻辑
// p和q在root的左右节点
if (left !== null && right !== null) {
return root;
} else if (left !== null && right === null) { // p和q都在根节点的右边
return left;
} else if (left === null && right !== null) { // p和q都在根节点的左边
return right;
} else { // 整棵树中都没有这里p和q
return null;
}
};/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* @param {TreeNode} root
* @param {TreeNode} p
* @param {TreeNode} q
* @return {TreeNode}
*/
/* 迭代法 */
var lowestCommonAncestor = function(root, p, q) {
let parentMap = new Map(); // 记录每个结点的父结点
let queue = []; // 用于层序遍历的队列
parentMap.set(root, null);
queue.push(root);
// 层序遍历,记录每个结点的父结点
while (!parentMap.has(p) || !parentMap.has(q)) {
let node = queue.shift();
if (node.left) {
parentMap.set(node.left, node);
queue.push(node.left);
}
if (node.right) {
parentMap.set(node.right, node);
queue.push(node.right);
}
}
let ancestors = new Set(); // 存储祖先结点
// 找到p的最近公共祖先
while (!ancestors.has(p)) {
ancestors.add(p);
p = parentMap.get(p);
}
// 找到与q最近的公共祖先
while (!ancestors.has(q)) {
q = parentMap.get(q);
}
return q;
};技巧总结
二叉搜索树
二叉搜索树是有数值的,二叉搜索树是一个有序树。
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 它的左、右子树也分别为二叉排序树
二叉搜索树的中序遍历是按升序排列的。
700 二叉搜索树中的搜索
给定二叉搜索树(BST)的根节点 root 和一个整数值 val。
你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在,则返回 null 。
示例 1:

输入:root = [4,2,7,1,3], val = 2
输出:[2,1,3]
示例2:

输入:root = [4,2,7,1,3], val = 5
输出:[]
提示:
数中节点数在 [1, 5000] 范围内
1 <= Node.val <= 107
root 是二叉搜索树
1 <= val <= 107
二叉搜索树的中序遍历是有序的(升序),根据BST的这一特点,使用中序遍历,找到根节点或者找到节点时就返回这个节点。
(1)递归
/**
* @param {TreeNode} root
* @param {number} val
* @return {TreeNode}
*/
var searchBST = function(root, val) {
if (root === null || root.val === val) {
return root;
}
if (root.val > val) {
return searchBST(root.left, val);
}
if (root.val < val) {
return searchBST(root.right, val);
}
};(2)迭代
/**
* @param {TreeNode} root
* @param {number} val
* @return {TreeNode}
*/
var searchBST = function(root, val) {
// BST的特点,搜索一个节点的路径是固定好的,不需要像二叉树那样需要回溯
while (root !== null) {
if (root.val < val) {
root = root.right;
} else if (root.val > val) {
root = root.left;
} else {
return root;
}
}
return null;
};98 验证二叉搜索树
二叉搜索树的中序遍历是有序的(升序),根据BST的这一特点,使用中序遍历,比较当前节点与前一个节点的值。
- 递归(设定一个最大值)
- 递归(记录当前节点的前一个节点)
- 迭代(中序遍历)
(统一模板的中序遍历没有实现)
(1)递归(设定一个最大值)
/**
* @param {TreeNode} root
* @return {boolean}
*/
var isValidBST = function(root) {
// 中序遍历位置---BST的中序遍历是有序的(升序)
let maxVal = -Infinity;
const inorder = (root) => {
if (root === null) {
return true;
}
let left = inorder(root.left);
// 中序遍历是否是升序的,如果不是就返回false
if (maxVal < root.val) {
maxVal = root.val;
} else {
return false;
}
let right = inorder(root.right);
return left && right;
}
return inorder(root);
};(2)递归(记录当前节点的前一个节点)
/**
* @param {TreeNode} root
* @return {boolean}
*/
var isValidBST = function(root) {
// 中序遍历位置---BST的中序遍历是有序的(升序)
// 如果节点的值非常小,这个时候用左边节点的值来进行比较
// let maxVal = -Infinity;
let pre = null;
const inorder = (root) => {
if (root === null) {
return true;
}
let left = inorder(root.left);
if (pre !== null && pre.val >= root.val) {
return false;
}
pre = root;
let right = inorder(root.right);
return left && right;
}
return inorder(root);
};(3)迭代
/**
* @param {TreeNode} root
* @return {boolean}
*/
var isValidBST = function(root) {
if (root === null) {
return true;
}
let stack = [];
let cur = root;
let pre = null;
while (cur !== null || stack.length) {
if (cur !== null) {
stack.push(cur);
cur = cur.left; // 左
} else {
// 中
cur = stack.pop();
if (pre !== null && cur.val <= pre.val) {
return false;
}
pre = cur;
cur = cur.right; // 右
}
}
return true;
};530 二叉搜索树的最小绝对差
给你一个二叉搜索树的根节点 root ,返回 树中任意两不同节点值之间的最小差值 。
差值是一个正数,其数值等于两值之差的绝对值。
示例 1:

输入:root = [4,2,6,1,3]
输出:1
示例 2:

输入:root = [1,0,48,null,null,12,49]
输出:1
提示:
树中节点的数目范围是 [2, 10^4]
0 <= Node.val <= 10^5
BST的中序遍历是有序的,最小的差肯定存在于相邻两个节点之差。
- 记录中序遍历结果,然后for循环遍历得到最小差;(时间复杂度高)
- 在中序遍历过程中,比较前一个节点与当前节点的差,一次遍历得到结果;
(1)中序遍历+for循环
/**
* @param {TreeNode} root
* @return {number}
*/
var getMinimumDifference = function(root) {
let inorder = [];
let result = Infinity;
// 中序遍历
const traverse = (node) => {
if (node === null) {
return ;
}
traverse(node.left);
inorder.push(node.val);
traverse(node.right);
}
traverse(root);
// console.log(inorder);
// 求任意两个节点的最小差值
for (let i = 1; i < inorder.length; i++) {
result = Math.min(result, inorder[i] - inorder[i - 1]);
}
return result;
};(2)pre和cur比较(递归和迭代)
/**
* @param {TreeNode} root
* @return {number}
*/
var getMinimumDifference = function(root) {
let pre = null;
let result = Infinity;
// 中序遍历-pre记录前一个节点
// 最小差肯定是相邻两个节点的值之差
const traverse = (cur) => {
if (cur === null) {
return ;
}
traverse(cur.left);
if (pre !== null) {
result = Math.min(result, cur.val - pre.val);
}
pre = cur;
traverse(cur.right);
}
traverse(root);
return result;
};/**
* @param {TreeNode} root
* @return {number}
*/
var getMinimumDifference = function(root) {
let pre = null;
let result = Infinity;
let stack = [];
let cur = root;
// 中序遍历-pre记录前一个节点
// 最小差肯定是相邻两个节点的值之差
while (cur !== null || stack.length) {
if (cur !== null) {
stack.push(cur);
cur = cur.left; // 左
} else {
cur = stack.pop(); // 中
if (pre !== null) {
result = Math.min(result, cur.val - pre.val);
}
pre = cur; // 记录前一个节点
cur = cur.right; // 右
}
}
return result;
};501 二叉搜索树中的众数
给你一个含重复值的二叉搜索树(BST)的根节点 root ,找出并返回 BST 中的所有 众数(即,出现频率最高的元素)。
如果树中有不止一个众数,可以按 任意顺序 返回。
假定 BST 满足如下定义:
结点左子树中所含节点的值 小于等于 当前节点的值
结点右子树中所含节点的值 大于等于 当前节点的值
左子树和右子树都是二叉搜索树
示例 1:

输入:root = [1,null,2,2]
输出:[2]
示例 2:
输入:root = [0]
输出:[0]
提示:
树中节点的数目在范围 [1, 104] 内
-10^5 <= Node.val <= 10^5
出现频率次数最多的是众数。设最大的出现频率是m,可能有多个节点出现的次数都为m。
还是利用BST中序遍历有序的特点,统计每个节点出现的次数,把最大次数的节点加入到结果中。
(1)迭代
/**
* @param {TreeNode} root
* @return {number[]}
*/
var findMode = function(root) {
let pre = null; // 前一个节点
let result= []; // 结果集
let count = 0; // 出现次数
let maxCount = 0; // 最大出现次数
// 中序遍历,利用BST中序遍历是有序的特点
const traverse = (cur) => {
if (cur === null) {
return null;
}
traverse(cur.left);
if (pre === null) { // 第一个节点
count = 1;
} else if (cur.val === pre.val) { // 与上一个节点数值相同的节点
count++;
} else { // 与上一个节点数值不同的节点
count = 1;
}
// 更新上一个节点
pre = cur;
// 判断该节点出现的频率是否是最大频率
if (count === maxCount) {
result.push(cur.val);
} else if (count > maxCount) {
// 如果当前节点的频率大于最大频率,更新最大频率,并将之前的result清空,放入当前最大频率的节点
maxCount = count;
result = [];
result.push(cur.val);
}
traverse(cur.right);
// return ;
}
traverse(root);
return result;
};236 二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
示例 1:

输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出:3
解释:节点 5 和节点 1 的最近公共祖先是节点 3 。
示例 2:

输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出:5
解释:节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。
示例 3:
输入:root = [1,2], p = 1, q = 2
输出:1
提示:
- 树中节点数目在范围 [2, 105] 内。
- -109 <= Node.val <= 109
- 所有 Node.val 互不相同 。
- p != q
- p 和 q 均存在于给定的二叉树中。
两个节点的最近公共祖先分为两种情况:
(1)两个节点分布在某个节点的两侧,这该节点是最近公共祖先;
(2)两个节点在同侧,则最上层的节点是最近公共祖先。
(1)递归
/**
* @param {TreeNode} root
* @param {TreeNode} p
* @param {TreeNode} q
* @return {TreeNode}
*/
var lowestCommonAncestor = function(root, p, q) {
// 2. 确定递归终止条件(找到p或q就返回)
if (root === p || root === q || root === null) {
return root;
}
// 1. 确定递归函数返回值和参数(后序)
let left = lowestCommonAncestor(root.left, p, q);
let right = lowestCommonAncestor(root.right, p, q);
// 3. 确定单层逻辑
if (left !== null && right !== null) { // p和q在两侧,返回此时的根节点
return root;
} else if (left!== null && right === null) { // p和q在同侧,则最上面的节点是最近公共祖先
return left;
} else if (left === null && right !== null) {
return right;
} else {
return null;
}
};(2)迭代(两个节点到根节点的路径的第一个交点,用map存储每个节点的父节点,然后找到p的所有祖先ancestors ,再从ancestors 中找离q最近的祖先)
/**
* @param {TreeNode} root
* @param {TreeNode} p
* @param {TreeNode} q
* @return {TreeNode}
*/
var lowestCommonAncestor = function(root, p, q) {
let parentMap = new Map(); // 记录每个结点的父结点
let queue = []; // 用于层序遍历的队列
parentMap.set(root, null);
queue.push(root);
// 层序遍历,记录每个结点的父结点
while (!parentMap.has(p) || !parentMap.has(q)) {
let node = queue.shift();
if (node.left) {
parentMap.set(node.left, node);
queue.push(node.left);
}
if (node.right) {
parentMap.set(node.right, node);
queue.push(node.right);
}
}
let ancestors = new Set(); // 存储祖先结点
// 找到p的所有祖先
while (!ancestors.has(p)) {
ancestors.add(p);
p = parentMap.get(p);
}
// 找到与p最近的公共祖先
while (!ancestors.has(q)) {
q = parentMap.get(q);
}
return q;
};
701 二叉搜索树中的插入操作
给定二叉搜索树(BST)的根节点 root 和要插入树中的值 value ,将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ,新值和原始二叉搜索树中的任意节点值都不同。
注意,可能存在多种有效的插入方式,只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。
示例 1:

输入:root = [4,2,7,1,3], val = 5
输出:[4,2,7,1,3,5]
解释:另一个满足题目要求可以通过的树是:
示例 2:
输入:root = [40,20,60,10,30,50,70], val = 25
输出:[40,20,60,10,30,50,70,null,null,25]
示例 3:
输入:root = [4,2,7,1,3,null,null,null,null,null,null], val = 5
输出:[4,2,7,1,3,5]
提示:
树中的节点数将在 [0, 10^4]的范围内。
-10^8 <= Node.val <= 10^8
所有值 Node.val 是 独一无二 的。
-10^8 <= val <= 10^8
保证 val 在原始BST中不存在。
- 在有空位置的时候返回新插入的节点,作为上一层的子节点。(递归有返回值)
- parent记录上一个访问的节点,cur记录当前访问的节点,插入的节点值小于parent.val就添加为parent的左子节点,插入节点的值大于parent.val就添加为parent的右子节点。
- 迭代的思路与2一样。
(1)递归有返回值
/**
* @param {TreeNode} root
* @param {number} val
* @return {TreeNode}
*/
var insertIntoBST = function(root, val) {
// 找到空的位置,插入结点
if (root === null) return new TreeNode(val, null, null);
// 插入值大于当前结点的值,将插入值插入到当前结点的右子树上
if (root.val < val) {
root.right = insertIntoBST(root.right, val);
}
// 插入值小于当前结点的值,将插入值插入到当前结点的左子树上
else if (root.val > val) {
root.left = insertIntoBST(root.left, val);
}
return root;
};(2)递归没有返回值
/**
* @param {TreeNode} root
* @param {number} val
* @return {TreeNode}
*/
var insertIntoBST = function(root, val) {
let parentNode = root;
if (root === null) {
return new TreeNode(val);
}
// 前序递归,没有返回值
const traverse = (cur, val) => {
if (cur === null) {
let node = new TreeNode(val);
if (val < parentNode.val) {
parentNode.left = node;
} else {
parentNode.right = node;
}
return ;
}
parentNode = cur;
if (val < cur.val) {
traverse(cur.left, val);
}
if (val > cur.val) {
traverse(cur.right, val);
}
return ;
}
traverse(root, val);
return root;
};(3)迭代法
/**
* @param {TreeNode} root
* @param {number} val
* @return {TreeNode}
*/
var insertIntoBST = function(root, val) {
// 迭代法
if (root === null) {
return new TreeNode(val);
}
let cur = root, pre = null;
// 找到插入的位置
while (cur !== null) {
pre = cur; // 记录上一个节点
if (val < cur.val) {
cur = cur.left;
} else {
cur = cur.right;
}
}
// 判断插入值与pre的值的大小
let node = new TreeNode(val);
if (val < pre.val) {
pre.left = node;
}
if (val > pre.val) {
pre.right = node;
}
return root;
};450 删除二叉搜索树中的节点
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:
首先找到需要删除的节点;
如果找到了,删除它。
示例 1:

输入:root = [5,3,6,2,4,null,7], key = 3
输出:[5,4,6,2,null,null,7]
解释:给定需要删除的节点值是 3,所以我们首先找到 3 这个节点,然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。
示例 2:
输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点
示例 3:
输入: root = [], key = 0
输出: []
提示:
节点数的范围 [0, 104].
-10^5 <= Node.val <= 10^5
节点值唯一
root 是合法的二叉搜索树
-10^5 <= key <= 10^5
分为五种情况:
第一种情况:没有找到要删除的节点,返回null;
找到了:
第二种情况:要删除的节点是叶子结点,返回null;
第三种情况:要删除的节点左子树为空,返回右子节点;
第四种情况:要删除的节点右子树为空,返回左子节点;
第五种情况:要删除的节点的左右子树都不为空,把左子树添加到右子树的最左边。
二叉树删除节点的通用解法:
- 交换要删除节点的值和右子树最左边的节点的值;
- 第二次访问到要删除节点(步骤一中交换的值),返回null给父节点(删除该节点)。
(1)二叉搜索树的递归解法
/**
* @param {TreeNode} root
* @param {number} key
* @return {TreeNode}
*/
var deleteNode = function(root, key) {
// 没找到值为key的节点
if (root === null) {
return root;
}
// 找到值为key的节点
if (root.val === key) {
// 第一种情况
if (root.left === null && root.right === null) {
return null;
} else if (root.left === null) { // 第二种情况
return root.right;
} else if (root.right === null) { // 第三种情况
return root.left;
} else { // 第四种情况
let cur = root.right;
while (cur.left !== null) {
cur = cur.left;
}
cur.left = root.left;
return root.right;
}
}
// 上一层的root接住返回值
if (key < root.val) {
root.left = deleteNode(root.left, key);
}
if (key > root.val) {
root.right = deleteNode(root.right, key);
}
return root;
};(2)二叉树删除的通用解法
/**
* @param {TreeNode} root
* @param {number} key
* @return {TreeNode}
*/
var deleteNode = function(root, key) {
// 二叉树删除节点的通用写法
if (root === null) {
return root;
}
if (root.val === key) {
if (root.right === null) {
return root.left; // 第二次处理,返回的是null
}
// 第一次处理,交换值
let cur = root.right;
while (cur.left) {
cur = cur.left;
}
[root.val, cur.val] = [cur.val, root.val];
}
// 接住下层节点返回的值
root.left = deleteNode(root.left, key);
root.right = deleteNode(root.right, key);
return root;
};
二叉树插入,删除的小结
插入操作和删除操作的递归写法中都用到了一种写法:返回一个值,然后上一层的节点接住这个值。
230 二叉搜索树中第K小的元素

二叉搜索树(Binary Search Tree,BST),BST 的中序遍历结果是有序的(升序)。这道题的逻辑代码在中序遍历位置,从中序遍历结果中找到第k小的元素,此时的时间复杂度为O(N)。
/** * Definition for a binary tree node. * function TreeNode(val, left, right) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } */ /** * @param {TreeNode} root * @param {number} k * @return {number} */ var kthSmallest = function(root, k) { /* BST的中序遍历结果是从小到大排列的 */ // 记录结果 let result = 0; // 当前元素的排名 let currentRank = 0; const select = (root, k) => { // 退出条件 if (!root) return null; select(root.left, k); // 中序遍历位置 currentRank++; // 找到第K个最小元素 if (currentRank === k) { result = root.val; return ; } select(root.right, k); } select(root, k); return result; }优化:根据BST的定义,结点的左子树小,右子树大。给每个节点添加一个额外信息,自己的排名m,每次搜索的时候比较k与m的大小,如果k<m就去当前结点的左子树去搜索k;如果k>m就去右子树搜索k。
优化后的时间复杂度为O(logN)。
538 1038 把二叉搜索树转换为累加树

BST的中序遍历结果性质很重要。并且,由于是中序遍历,所以在对根节点做操作时,逻辑处理代码是在
中序遍历位置。var convertBST = function(root) { // 记录累加和 let sum = 0; const traverse = root => { // 退出条件 if (root === null) return null; // 迭代右子树 traverse(root.right); // 中序遍历位置 sum += root.val; root.val = sum; // 迭代左子树 traverse(root.left); } traverse(root); return root; };
96 不同的二叉搜索树

穷举+递归的解法
/**
* @param {number} n
* @return {number}
*/
var numTrees = function(n) {
return count(1, n);
};
// 穷举不同的BST
/**
* @param {number} low 最小的结点值
* @param {number} hight 最大的结点值
*/
function count(low, hight) {
// 退出条件
if (low > hight) return 1;
// 保存不同的BST个数的变量
let result = 0;
// 穷举BST的个数
for (let i = low; i <= hight; i++) {
// i作为根结点的左子树中BST的组合个数
let left = count(low, i - 1);
let right = count(i + 1, hight);
// BST的个数=根节点左子树BST组合个数*根节点右子树BST组合个数
result += left * right;
}
return result;
}95 不同的二叉搜索树 II

找到不同BST的组合
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {number} n
* @return {TreeNode[]}
*/
var generateTrees = function(n) {
if (n === 0) {
return [];
}
return generate(1, n);
};
function generate(low, high) {
let result = [];
// 此时没有数字,直接返回
if (low > high) {
result.push(null);
return result;
}
// 只有一个数字,将这个数字作为根结点,然后加入结果列表中
// if (low === high) {
// let root = new TreeNode(low);
// result.push(root);
// return result;
// }
// 此时,将(low, high)中的所有数字都作为根结点,然后递归得到每一种组合
// 遍历每种可能
for (let i = low; i <= high; i++) {
// 根节点的左子树构成的BSTs
let leftBSTs = generate(low, i - 1);
// 根结点的右子树构成的BSTs
let rightBSTs = generate(i + 1, high);
for (let letfBST of leftBSTs) {
for (let rightBST of rightBSTs) {
// 左BST和右BST接到根节点上
let root = new TreeNode(i);
root.left = letfBST;
root.right = rightBST;
result.push(root);
}
}
}
return result;
}1373. 二叉搜索子树的最大键值和

这道题的常规解题思路逻辑很清晰,但是算法复杂度高,递归嵌套递归,有空去实现一下,巩固基础。
优化的算法是后序遍历,借助一个额外的函数,通过一次递归得到根结点需要的数据。
对递归的理解越来越懵了,这是咋回事,要回头总结!!!
这个题还没吃透。
/* 后序遍历 */
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number}
*/
var maxSumBST = function(root) {
// 全部变量,记录最大值
let maxSum = 0;
/**
* 返回一个数组,记录根节点操作需要的信息
*
*/
function traverse(root) {
// base case
if (root === null) {
return [1, Number.MAX_SAFE_INTEGER, Number.MIN_SAFE_INTEGER, 0];
}
let left = traverse(root.left);
let right = traverse(root.right);
/* 后序遍历位置 */
let result = new Array(4);
// 判断以root为根的二叉树是不是BST
if (left[0] === 1 && right[0] === 1 && root.val > left[2] && root.val < right[1]) {
result[0] = 1;
// 这里大小判断是因为空结点返回的数组中的值的影响
// 左子树的最小值
result[1] = Math.min(left[1], root.val);
// 右子树的最大值
result[2] = Math.max(right[2], root.val);
// 求和
result[3] = left[3] + right[3] + root.val;
maxSum = Math.max(maxSum, result[3]);
} else {
// 以root为根的二叉树不是BST
result[0] = 0;
}
return result;
}
traverse(root);
return maxSum;
};
297 二叉树的序列化与反序列化

本质:二叉树的遍历和恢复。
这个题还没吃透。
前序遍历
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* Encodes a tree to a single string.
*
* @param {TreeNode} root
* @return {string}
*/
var serialize = function(root) {
// 定义在函数外面会出问题
let sequence = [];
const serializeHelper = (root) => {
/* 前序遍历 */
if (root === null) {
sequence.push('#');
return '#';
}
sequence.push(root.val);
serializeHelper(root.left);
serializeHelper(root.right);
}
serializeHelper(root);
return sequence.toString();
};
/**
* Decodes your encoded data to tree.
*
* @param {string} data
* @return {TreeNode}
*/
var deserialize = function(data) {
if (data === '#') {
// 这里必须返回null,返回空结点通不过
return null;
}
let nodes = data.split(',');
const deserializeHelper = (nodes) => {
if (nodes.length === 0) {
return null;
}
let firstVal = nodes.shift(0);
if (firstVal === '#') {
return null;
}
let root = new TreeNode(parseInt(firstVal));
root.left = deserializeHelper(nodes);
root.right = deserializeHelper(nodes);
return root;
}
return deserializeHelper(nodes);
};
/**
* Your functions will be called as such:
* deserialize(serialize(root));
*/
后序遍历
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* Encodes a tree to a single string.
*
* @param {TreeNode} root
* @return {string}
*/
var serialize = function(root) {
let sequence = [];
const traverse = root => {
if (root === null) {
sequence.push('#');
return null;
}
// 后序遍历
traverse(root.left);
traverse(root.right);
sequence.push(root.val);
}
traverse(root);
return sequence.toString();
};
/**
* Decodes your encoded data to tree.
*
* @param {string} data
* @return {TreeNode}
*/
var deserialize = function(data) {
let nodes = data.split(',');
const deTraverse = nodes => {
lastVal = nodes.pop();
if (lastVal === '#') {
return null;
}
let root = new TreeNode(lastVal);
root.right = deTraverse(nodes);
root.left = deTraverse(nodes);
return root;
}
let root = deTraverse(nodes);
return root;
};
/**
* Your functions will be called as such:
* deserialize(serialize(root));
*/层序遍历
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* Encodes a tree to a single string.
*
* @param {TreeNode} root
* @return {string}
*/
var serialize = function(root) {
let sequence = [];
if (root === null) {
sequence.push('#');
return sequence.toString();
}
// 定义一个队列存放当前结点的非空左右子树
let queue = [];
queue.push(root);
// 层序遍历
while (queue.length != 0) {
let currentNode = queue.shift();
if (currentNode === null) {
sequence.push('#');
continue;
}
sequence.push(currentNode.val);
queue.push(currentNode.left);
queue.push(currentNode.right);
}
return sequence.toString();
};
/**
* Decodes your encoded data to tree.
*
* @param {string} data
* @return {TreeNode}
*/
var deserialize = function(data) {
// console.log(data);
if(data === '#') return null;
let nodes = data.split(',');
// 二叉树的根结点
let root = new TreeNode(nodes[0]);
// 队列中都存放非空的根结点
let queue = [];
queue.push(root);
// 层序遍历
for (let i = 1; i < nodes.length; ) {
// 从队列中出队一个根结点
let parentNode = queue.shift();
// 父结点对应的左孩子的值在父结点右边第一个,然后i(当做指针)往后移动一个位置,指向父结点的右孩子的值
let left = nodes[i++];
if (left != '#') {
parentNode.left = new TreeNode(parseInt(left));
// 将非空结点入队
queue.push(parentNode.left);
} else {
parentNode.left = null;
}
// 指针i向后移动到下一个结点
let right = nodes[i++];
if (right != '#') {
parentNode.right = new TreeNode(parseInt(right));
queue.push(parentNode.right);
} else {
parentNode.right = null;
}
}
return root;
};
/**
* Your functions will be called as such:
* deserialize(serialize(root));
*/技巧总结
链表
203 移除链表元素

- 直接在链表上操作
- 虚拟头节点
直接在原链表上操作
/**
* Definition for singly-linked list.
* function ListNode(val, next) {
* this.val = (val===undefined ? 0 : val)
* this.next = (next===undefined ? null : next)
* }
*/
/**
* @param {ListNode} head
* @param {number} val
* @return {ListNode}
*/
var removeElements = function(head, val) {
// 链表中的所有元素都要删除
while (head !== null && head.val === val) {
head = head.next;
}
// 链表为空
if (head === null) {
return null;
}
// 此时说明不再删头节点了
// 指向前一个节点
let pre = head;
// 指向当前的节点
let cur = head.next;
while (cur !== null) {
if (cur.val === val) {
pre.next = cur.next;
} else {
pre = cur;
}
// 指向下一个节点
cur = cur.next;
}
return head;
};虚拟头节点
/**
* Definition for singly-linked list.
* function ListNode(val, next) {
* this.val = (val===undefined ? 0 : val)
* this.next = (next===undefined ? null : next)
* }
*/
/**
* @param {ListNode} head
* @param {number} val
* @return {ListNode}
*/
var removeElements = function(head, val) {
if (head === null) {
return null;
}
// 定义一个虚拟头节点
let dummyNode = new ListNode(null, head);
// 定义一个指针指向当前节点
let cur = dummyNode;
while(cur.next) {
if (cur.next.val === val) {
// 删除下一个节点
cur.next = cur.next.next;
continue;
} else {
// 指针指向下一个节点
cur = cur.next;
}
}
return dummyNode.next;
};707 设计链表

对链表的增删查改,是对链表操作的综合考察。
细节上的问题:
- 头节点同时是尾节点的情况;
- size什么时候加和减,加了几次;
- 删除index位置节点容易出错;
/**
* 定义节点
*/
class LinkNode {
constructor (val, next) {
this.val = val;
this.next = next;
}
}
/**
* 单链表,存储头节点和尾节点以及节点数量
*/
var MyLinkedList = function() {
this._size = 0;
this._head = null;
this._tail = null;
};
/**
* 获取链表index位置的节点
*/
MyLinkedList.prototype.getNode = function (index) {
if (index < 0 || index >= this._size) {
return null;
}
// 创建虚拟头节点
let cur = new LinkNode(0, this._head);
while(index-- >= 0) {
cur = cur.next;
}
// console.log(cur);
return cur;
}
/**
* @param {number} index
* @return {number}
*/
MyLinkedList.prototype.get = function(index) {
if (index < 0 || index >= this._size) {
return -1;
}
// console.log(index);
return this.getNode(index).val;
};
/**
* @param {number} val
* @return {void}
*/
MyLinkedList.prototype.addAtHead = function(val) {
let node = new LinkNode(val, this._head);
this._head = node;
this._size++;
// 如果还没有添加尾节点
if (!this._tail) {
this._tail = node;
}
};
/**
* @param {number} val
* @return {void}
*/
MyLinkedList.prototype.addAtTail = function(val) {
this._size++;
let node = new LinkNode(val, null);
// 如果尾节点不为空
if (this._tail) {
this._tail.next = node;
this._tail = node;
} else {
// 如果尾节点为空,则头节点也为空,此时还没有添加节点
this._tail = node;
this._head = node;
}
};
/**
* @param {number} index
* @param {number} val
* @return {void}
*/
MyLinkedList.prototype.addAtIndex = function(index, val) {
if (index <= 0) {
this.addAtHead(val);
return ;
} else if (index === this._size) {
this.addAtTail(val);
return ;
} else if (index > this._size) {
return ;
} else {
let preNode = this.getNode(index -1);
let newNode = new LinkNode(val, preNode.next);
preNode.next = newNode;
}
this._size++;
};
/**
* @param {number} index
* @return {void}
*/
MyLinkedList.prototype.deleteAtIndex = function(index) {
if (index < 0 || index >= this._size) {
return ;
}
// index有效
if (index === 0) {
this._head = this._head.next;
// 如果头节点同时也是尾节点
if (index == this._size - 1) {
this._tail = this._head;
}
} else {
let preNode = this.getNode(index - 1);
preNode.next = preNode.next.next;
if (index === this._size - 1) {
this._tail = preNode;
}
}
// 删完之后size再减
this._size--;
};
/**
* Your MyLinkedList object will be instantiated and called as such:
* var obj = new MyLinkedList()
* var param_1 = obj.get(index)
* obj.addAtHead(val)
* obj.addAtTail(val)
* obj.addAtIndex(index,val)
* obj.deleteAtIndex(index)
*/206 反转链表

- 双指针法
用中间节点temp保存cur的next节点- 与双指针相同思路的递归
- 递归,从后往前翻转
- 难以理解,很考察对递归的理解程度;
- 👉动画演示+多种解法 206. 反转链表 - 反转链表 - 力扣(LeetCode) (leetcode-cn.com)
/**
* Definition for singly-linked list.
* function ListNode(val, next) {
* this.val = (val===undefined ? 0 : val)
* this.next = (next===undefined ? null : next)
* }
*/
/** 1. 双指针法
* @param {ListNode} head
* @return {ListNode}
*/
var reverseList = function(head) {
if (head === null) {
return null;
}
let pre = null;
let cur = head;
let temp = null;
while(cur !== null) {
temp = cur.next;
// 改变next方向
cur.next = pre;
// pre往后移动
pre = cur;
// cur往后移动
cur = temp;
}
return pre;
};/**
* Definition for singly-linked list.
* function ListNode(val, next) {
* this.val = (val===undefined ? 0 : val)
* this.next = (next===undefined ? null : next)
* }
*/
/**
* @param {ListNode} head
* @return {ListNode}
*/
var reverseList = function(head) {
return traverse1(null, head);
}
// 3. 与双指针相同思路的递归
function traverse1(pre, cur) {
if (cur === null) return pre;
let temp = cur.next;
cur.next = pre;
return traverse1(cur, temp);
}
/**
* Definition for singly-linked list.
* function ListNode(val, next) {
* this.val = (val===undefined ? 0 : val)
* this.next = (next===undefined ? null : next)
* }
*/
/** 3. 递归,从后往前翻转
* @param {ListNode} head
* @return {ListNode}
*/
var reverseList = function(head) {
// return traverse1(null, head);
return traverse2(head);
}
// 从后往前翻转(遍历完再翻转)
function traverse2(head) {
if (!head || !head.next) {
return head;
}
// 递归调用
let last = traverse2(head.next);
// 翻转头节点和第二个节点的方向
head.next.next = head;
head.next = null;
return last;
}24. 两两交换链表中的节点

画图,按照交换步骤组织代码逻辑
虚拟头节点法
/**
* Definition for singly-linked list.
* function ListNode(val, next) {
* this.val = (val===undefined ? 0 : val)
* this.next = (next===undefined ? null : next)
* }
*/
/**
* @param {ListNode} head
* @return {ListNode}
*/
var swapPairs = function(head) {
let dummyNode = new ListNode(0, head);
let cur = dummyNode;
while(cur.next !== null && cur.next.next !== null) {
let temp1 = cur.next;
let temp2 = cur.next.next.next;
// 步骤一
cur.next = cur.next.next;
// 步骤二
cur.next.next = temp1;
// 步骤三
cur.next.next.next = temp2;
// cur向后移动两个节点
cur = cur.next.next;
}
return dummyNode.next;
};19. 删除链表的倒数第 N 个结点

快慢指针+虚拟头节点(用了两次循环)
n: 要删除的倒数第n个节点;
L:链表的长度
- fast指针和slow指针首先指向dummy node;
- fast指针移动n+1个节点;
- slow指针移动L-n个节点,指向倒数第n个节点的前一个节点。(这里快慢指针一起移动,fast指针指向null时,停止移动)
- 删除slow.next = slow.next.next;
/**
* Definition for singly-linked list.
* function ListNode(val, next) {
* this.val = (val===undefined ? 0 : val)
* this.next = (next===undefined ? null : next)
* }
*/
/**
* @param {ListNode} head
* @param {number} n
* @return {ListNode}
*/
var removeNthFromEnd = function(head, n) {
// 创建虚拟头节点
let dummyNode = new ListNode(0, head);
// 定义双指针
let fast = slow = dummyNode;
// 1. fast移动n+1个节点
while(n-- && fast !== null) {
fast = fast.next;
}
fast = fast.next;
// slow移动的节点数量是:L+1-(n+1)=L-n, L表示链表长度
while(fast !== null) {
// 2. fast继续移动,直至指向null
fast = fast.next;
// 3. slow跟fast一起移动,指向待删除节点的前一个节点
slow = slow.next;
}
// 删除倒数第n个节点
slow.next = slow.next.next;
return dummyNode.next;
};160. 相交链表

lenA: 链表A的长度;
lenB: 链表B的长度;
- 定义一个获取链表长度的辅助函数;
- curA, curB分别指向headA和headB;
- 指定A为最长的链表,如果不是就交换;
- curA移动(lenA -lenB)个节点,与curB对齐;
- curA与curB同时移动,只要有curA===curB,退出循环,返回curA;
/**
* Definition for singly-linked list.
* function ListNode(val) {
* this.val = val;
* this.next = null;
* }
*/
/**
* @param {ListNode} headA
* @param {ListNode} headB
* @return {ListNode}
* 如果链表A和B相交,则从相交节点开始,后面的节点位置是对齐的
*/
var getIntersectionNode = function(headA, headB) {
// 定义指向当前节点的指针
let curA = headA;
let curB = headB;
let lenA = lenB = 0;
// 1. 获取链表长度
lenA = getListLength(curA);
lenB = getListLength(curB);
// 2. 比较链表A和B的长度,始终让A为最长的链表
if (lenA < lenB) {
[curA, curB] = [curB, curA];
[lenA, lenB] = [lenB, lenA];
}
let gap = lenA - lenB;
// 3. 移动curA,与curB的位置对齐
while(gap--) {
curA = curA.next;
}
// 4. 同时移动curA和curB并比较是否相交
while(curA && curA !== curB) {
curA = curA.next;
curB = curB.next;
}
return curA;
};
function getListLength(head) {
let len = 0;
let cur = head;
while (cur !== null) {
cur = cur.next;
len++;
}
return len;
}142. 环形链表 II

快慢指针法
- 先判断链表有没有环
- 定义快慢指针fast和slow分别指向头节点;
- fast指针每次移动2步,slow指针移动一步,如果相遇,则说明有环;如果没有环就返回null。
- 找到了相遇的节点。定义两个指针index1和index2,index1指向头节点,index2指向相遇的节点,然后index1和index2同时移动,步长都为1,当index1===index2时,此时两个指针指向的节点就是环的入口。

/**
* Definition for singly-linked list.
* function ListNode(val) {
* this.val = val;
* this.next = null;
* }
*/
/**
* @param {ListNode} head
* @return {ListNode}
*/
var detectCycle = function(head) {
/**
快慢指针法
*/
let fast = head;
let slow = head;
while (fast !== null && fast.next !== null) {
// 1. fast指针每次移动两个节点,slow指针每次移动一个节点
fast = fast.next.next;
slow = slow.next;
// 2. (判断是否有环)当fast与slow相遇时,再次定义两个指针,index1从相遇的节点出发,index2从头节点出发
if (slow === fast) {
let index1 = fast;
let index2 = head;
// 3. 当index1和index2相遇时,此时所在的节点就是环的入口节点
while (index1 !== index2) {
index1 = index1.next;
index2 = index2.next;
}
return index1;
}
}
// 3. 没有找到环
return null;
};技巧总结
- 虚拟头节点—在需要返回操作后的头节点时常用,不用管头节点的边界问题;
- 203 移除链表元素;
- 双指针—同时移动;
- 206 翻转链表
- 24 两两交换链表中的节点
- 160 相交链表
- 快慢指针—fast和slow;
- 判断有没有环(fast每次移动2,slow移动1);
- 删除倒数第n个节点,fast先移动n+1个节点,然后slow和fast一起移动,直到fast指向null,此时删除slow.next;
- 142 环形链表II
数组
- 704 二分查找
- 35 搜索插入位置
- 34 在排序数组中查找元素的第一个和最后一个位置
- 27 移除元素
- 209 长度最小的子数组
- 904 水果成篮
- 76 最小覆盖子串
- 59 螺旋矩阵
- 54 螺旋矩阵
704 二分查找

/**
* @param {number[]} nums
* @param {number} target
* @return {number}
*/
var search = function(nums, target) {
/**
闭合区间[left, right]
*/
let left = 0;
let right = nums.length - 1;
while (left <= right) {
// JS中除不尽的话不会自动舍出小数点,调用Math.floor
let middle = left + Math.floor((right - left) / 2);
// console.log(middle);
if (target < nums[middle]) {
right = middle - 1;
} else if (target > nums[middle]) {
left = middle + 1;
} else {
return middle;
}
}
return -1;
};35 搜索插入位置

- 二分查找法,注意返回值处理的4种插值情况。
- 暴力解法—循环
/**
* @param {number[]} nums
* @param {number} target
* @return {number}
*/
var searchInsert = function(nums, target) {
let left = 0;
let right = nums.length - 1;
let middle = 0;
while (left <= right) {
middle = left + Math.floor((right - left) / 2);
if (target < nums[middle]) {
right = middle - 1;
} else if (target > nums[middle]) {
left = middle + 1;
} else {
return middle;
}
}
return right + 1;
};/**
* @param {number[]} nums
* @param {number} target
* @return {number}
*/
var searchInsert = function(nums, target) {
for (let i = 0; i < nums.length; i++) {
/**
这里处理三种情况:
1. 插入位置在所有元素之前
2. 插入元素的数组中的值
3. 插入元素到数组中
*/
if (target <= nums[i]) {
return i;
}
}
return nums.length;
};34 在排序数组中查找元素的第一个和最后一个位置

- 分别找左边界,右边界。(最简单的思路—定义两个分别找左右边界的辅助函数)
难点在找左右边界时,如何确定最左边或最右边的target的索引。
/**
* @param {number[]} nums
* @param {number} target
* @return {number[]}
*/
var searchRange = function(nums, target) {
// target不在数组内
if(!nums.length || nums[0] > target || nums[nums.length - 1] < target) {
return [-1, -1];
}
let start = getLeftMargin(nums, target);
let end = getRightMargin(nums, target);
return [start, end];
};
/* 找target在数组nums中的左边界 */
function getLeftMargin(nums, target) {
let low = 0;
let high = nums.length - 1;
while (low <= high) {
let middle = low + Math.floor((high - low) / 2);
// 关键代码,即使找到了target在数组中的位置,也让high往左移动,而low不动
if (target === nums[middle]) {
high = middle - 1;
} else if (target < nums[middle]) {
high = middle - 1;
} else {
low = middle + 1;
}
}
if (nums[low] === target) {
return low;
} else {
return -1;
}
}
/* 找target在数组nums中的右边界 */
function getRightMargin(nums, target) {
let low = 0;
let high = nums.length - 1;
while (low <= high) {
let middle = low + Math.floor((high - low) / 2);
// 关键代码,即使找到了target在数组中的位置,也让low往右移动,而high不动
if (target === nums[middle]) {
low = middle + 1;
} else if (target > nums[middle]) {
low = middle + 1;
} else {
high = middle - 1;
}
}
if (nums[high] === target) {
return high;
} else {
return -1;
}
}27. 移除元素

快慢指针法
快慢指针同时移动,遇到要删除元素时,快指针继续往前移动,slow指针不动。之后就相当于要删除元素之后的元素往前移动一位,将要删除的元素覆盖掉。
/**
* @param {number[]} nums
* @param {number} val
* @return {number}
*/
var removeElement = function(nums, val) {
/* 快慢指针 */
let slowIndex = 0;
for (let fastIndex = 0; fastIndex < nums.length; fastIndex++) {
if (nums[fastIndex] !== val) {
nums[slowIndex] = nums[fastIndex];
slowIndex++;
}
}
return slowIndex;
};209 长度最小的子数组

- 暴力解法,双循环
不断从子数组中寻找满足条件的长度最小的子数组,找到满足条件的就break,从下一个子数组中找,直到退出循环。- 滑动窗口
这个解法太妙了,直接把时间复杂度降低一个量级
- 确定左边界,右边界
- 左边界移动,更新窗口内的值;
- 右边界移动,更新窗口内的值。
/**
* @param {number} target
* @param {number[]} nums
* @return {number}
*/
var minSubArrayLen = function(target, nums) {
/* 暴力解法 */
let result = Number.MAX_SAFE_INTEGER;
let subLength = 0; // 子数组的长度
let sum = 0; // 子数组元素的和
for (let i = 0; i < nums.length; i++) {
sum = 0;
for (let j = i; j < nums.length; j++) {
sum += nums[j];
// 满足条件,求出此时的子数组长度,然后与result比较
if (sum >= target) {
subLength = j - i + 1;
if (subLength < result) {
result = subLength;
}
break; // 只要找到了满足条件的子数组,让子数组长度与result对比并重新给result赋值后,跳出内循环,开始从下一个子数组中寻找
}
}
}
if (result === Number.MAX_SAFE_INTEGER) {
return 0;
}
return result;
};/**
* @param {number} target
* @param {number[]} nums
* @return {number}
*/
var minSubArrayLen = function(target, nums) {
/* 滑动窗口解法 */
let result = Number.MAX_SAFE_INTEGER;
let subLength = 0; // 滑动窗口的长度
let sum = 0; // 滑动窗口内元素的和
let i = 0; // 滑动窗口的左边界
for (let j = 0; j < nums.length; j++) {
sum += nums[j];
while (sum >= target) {
// 满足条件,求出此时的子数组长度,然后与result比较
if (sum >= target) {
subLength = j - i + 1;
result = subLength < result ? subLength : result;
/**
滑动窗口的核心代码,滑动窗口内的值减去左边界的值,左边界i向右移动一个位置,右边界向前移动,重复这个过程
*/
sum -= nums[i++]
}
}
}
if (result === Number.MAX_SAFE_INTEGER) {
return 0;
}
return result;
};904 水果成篮

滑动窗口法
使用滑动窗口方法要确定:
- 窗口中装的什么—两种不同种类的水果;
- 窗口左边界如何移动,什么时候移动;
- 窗口右边界如何移动
/**
* @param {number[]} fruits
* @return {number}
*/
var totalFruit = function(fruits) {
let left = 0; // 窗口左边界
let fruitWindow = new Map(); // 滑动窗口,存储每一种水果装入篮中的个数
fruitWindow.set(fruits[left], 1); // 窗口左边界的水果入篮
let count = 1; // 记录窗口内水果的种类数量
let maxLength = 1; // 窗口的最大长度
// 外层循环---窗口=右边界移动
for (let right = 1; right < fruits.length; right++) {
// 窗口内没有存过这种水果,或者这种水果在篮中的个数为0
if (!fruitWindow.get(fruits[right]) || fruitWindow.get(fruits[right]) === 0) {
fruitWindow.set(fruits[right], 1);
count++;
} else {
// 存过这种水果,直接数量+1
fruitWindow.set(fruits[right], fruitWindow.get(fruits[right]) + 1);
}
// 当满足篮中水果种类数小于2时,更新最大窗口长度
if (count <= 2) {
maxLength = right - left + 1 > maxLength ? right - left + 1 : maxLength;
}
// 内部循环,当不满足条件时,左边界向右移动,直到满足条件。
// 左边界移动,判断左边界所在位置的水果数量是否为0,为0说明篮中没有这种水果了,count-1
while (count > 2) {
// 左边界处的水果数-1
fruitWindow.set(fruits[left], fruitWindow.get(fruits[left]) - 1);
// 更新count
if (fruitWindow.get(fruits[left]) === 0) {
count--;
}
// 左边界右移
left++;
}
}
return maxLength;
};76 最小覆盖子串

滑动窗口
左边界,右边界 区间是怎样的
窗口在什么时候更新数据,什么时候移动左边界,什么时候更新结果
/**
* @param {string} s
* @param {string} t
* @return {string}
*/
/* 滑动窗口,左闭右开[left, right),初始时窗口内没有数据 */
var minWindow = function(s, t) {
let left = 0; // 左边界
let myWindow = new Map(); // 滑动窗口
let need = {}; // 将目标子串的中的字符转换成map,存储key: char, value: count(char)
let valid = 0; // 窗口满足条件的不同字符个数和
let start = 0; // 最小子串的左边界
let len = Number.MAX_SAFE_INTEGER; // 最小子串的长度
// need赋值
for (let char of t) {
need[char] = need[char] === undefined ? 1 : need[char] + 1;
}
// console.log(need)
// 右边界右移
for (let right = 0; right < s.length; right++) {
// 待移入窗口的字符
let charR = s[right];
// 更新窗口内数据
// charR是否为满足条件的字符
if (need[charR]) {
// 窗口内右边界指向的字符个数+1
myWindow.set(charR, myWindow.get(charR) === undefined ? 1 : myWindow.get(charR) + 1);
// 窗口内的charR跟need中的个数一致,valid+1
if (need[charR] === myWindow.get(charR)) {
valid++;
}
}
// 窗口内的字符满足条件,左边界右移
while (valid === Object.getOwnPropertyNames(need).length) {
// 待移出窗口的字符
let charL = s[left];
// 更新结果
if (right - left < len) {
start = left;
len = right - left;
}
if (need[charL]) {
// 相同的字符,就将valid-1
if (need[charL] === myWindow.get(charL)) {
valid--;
}
//
myWindow.set(charL, myWindow.get(charL) - 1);
}
left++;
}
}
// console.log(start, start + len);
return len === Number.MAX_SAFE_INTEGER ? "" : s.slice(start, start + len + 1);
};59 螺旋矩阵

给n赋几个值,然后观察规律。
- 得到螺旋数组的过程,这个过程都涉及哪些变量;
- 循环的每一条边,保持区间变量一致,即左闭右开
/**
* @param {number} n
* @return {number[][]}
*/
var generateMatrix = function(n) {
let loopCount = Math.floor(n / 2); // 循环的圈数
let startX = startY = 0; // 循环开始的位置
let middle = Math.floor(n / 2); // 如果n为奇数要手动填充中间位置的值
let offset = 1; // 控制每一圈循环的边界
let count = 1; // 控制数值增加
// console.log(loopCount, middle);
// JavaScript创建二维数组的一种方式
let matrix = new Array(n);
for (let i = 0; i < n; i++) {
matrix[i] = new Array(n);
}
// console.log(matrix);
let i = j = 0;
while(loopCount--) {
i = startX;
j = startY;
// 上方从右到左
for (; j < n - offset; j++) {
matrix[i][j] = count;
count++;
}
// 右方从上到下
for (; i < n - offset; i++) {
matrix[i][j] = count;
count++;
}
// 下方从右到左
for (; j > startY; j--) {
matrix[i][j] = count;
count++;
}
// 左方从下到上
for (; i > startX; i--) {
matrix[i][j] = count;
count++;
}
// 循环一圈了,更新下一圈的开始位置
startX++;
startY++;
// 更新控制右边界的变量
offset++;
}
// 奇数填充中间位置的值
if (n % 2 !== 0) {
matrix[middle][middle] = n * n;
}
return matrix;
};54 螺旋矩阵

循环的区间–左开右闭
当m===n时,正常
当m !== n时{
循环的次数由小的那个数决定;
循环里面要判断边界,是否还需要剩下两个方向的遍历。
}
/**
* @param {number[][]} matrix
* @return {number[]}
*/
var spiralOrder = function(matrix) {
let m = matrix.length;
let n = matrix[0].length;
let startX = startY = 0;
let loopCount = m < n ? Math.ceil(m / 2) : Math.ceil(n / 2);
let middle = Math.floor(m / 2);
let offset = 1;
let result = [];
// console.log(m, n);
if (m === 1) {
return matrix[0];
} else if (n === 1) {
matrix.forEach(item => {
result.push(item[0])
})
return result;
}
let i = j = 0;
while(loopCount--) {
i = startX;
j = startY;
// 上方从左到右
for (; j < n - offset; j++) {
result.push(matrix[i][j]);
}
// 右方从上到下
for (; i < m - offset; i++) {
result.push(matrix[i][j]);
}
if (m != n) {
if (n - offset === startY) {
result.push(matrix[i][j]);
continue;
} else if (m - offset === startX) {
result.push(matrix[i][j]);
continue;
}
}
// 下方从右到左
for (; j > startY; j--) {
result.push(matrix[i][j]);
}
// 左边从下到上
for (; i > startX; i--) {
result.push(matrix[i][j]);
}
// 走完一圈,更新开始循环的位置
startX++;
startY++;
// offset更新(控制边界)
offset++;
}
if (m === n && m % 2 !== 0) {
result.push(matrix[middle][middle]);
}
return result;
};技巧总结
二分查找—
middle = left + Math.floor((right - left) / 2), 闭合区间[left, right];快慢指针—初始时,fast和slow指向同一个位置,然后同时移动,满足某个条件时,fast指针继续移动,slow不动。
- 27 移除元素
滑动窗口—窗口内装什么值,右边界什么时候更新窗口的值,左边界什么时候移动,怎么更新窗口内的值;
209 长度最小的子数组
904 水果成篮
76 最小覆盖子串
螺旋矩阵—保持区间左闭右开,四个方向;
- 当m×n的矩阵,m=== n时是最简单的,当m !== n时,在循环内部判断特殊情况;
- 涉及的变量:
- middle(当m===n且m,n是奇数时,单独处理)
- loopCount(循环的圈数)
- startX, startY(循环的起点)
- offset(更新边界时用到)
- 当m === n时,
loopCount = Math.floor(n / 2); - 当m !== n时,
loopCount = m < n ? Math.ceil(m / 2) : Math.ceil(n / 2);
栈和队列
232 用栈实现队列

- 用两个栈模拟队列,stackA是输入栈,存储输入的数据,stackB是输出栈,用于模拟队列的输出;
- 注意pop和peek的代码细节。
var MyQueue = function() {
this.stackA = []; // 输入栈
this.stackB = []; // 输出栈
};
/**
* @param {number} x
* @return {void}
*/
MyQueue.prototype.push = function(x) {
this.stackA.push(x);
};
MyQueue.prototype.switchStackAAndB = function () {
while (this.stackA.length) {
this.stackB.push(this.stackA.pop());
}
};
/**
* @return {number}
*/
MyQueue.prototype.pop = function() {
const size = this.stackB.length;
if (size) {
return this.stackB.pop();
} else {
if (this.stackA.length) {
this.switchStackAAndB();
return this.stackB.pop();
}
}
return null;
};
/**
* @return {number}
*/
MyQueue.prototype.peek = function() {
// 输出栈stackB先出队,再入队,这里复用了pop的代码
const x = this.pop()
this.stackB.push(x)
return x;
};
/**
* @return {boolean}
*/
MyQueue.prototype.empty = function() {
// !(this.stackA.length || this.stackB.length)
return !this.stackA.length && !this.stackB.length;
};
/**
* Your MyQueue object will be instantiated and called as such:
* var obj = new MyQueue()
* obj.push(x)
* var param_2 = obj.pop()
* var param_3 = obj.peek()
* var param_4 = obj.empty()
*/225 用队列实现栈

JavaScript模拟队列—数组+push+shift
一个队列模拟栈
/* 两个队列模拟栈 */
var MyStack = function() {
this.queueOut = []; // 输出队列
this.queueBackup = []; // 备份队列
};
/**
* @param {number} x
* @return {void}
*/
MyStack.prototype.push = function(x) {
this.queueOut.push(x);
};
/**
* @return {number}
*/
MyStack.prototype.pop = function() {
let value = null;
let sizeOut = this.queueOut.length;
let sizeBackup = 0;
if (sizeOut) {
sizeOut--; // 保留queueOut队尾的元素
// 将queueOut队尾之前的元素备份到queueBack
while (sizeOut--) {
this.queueBackup.push(this.queueOut.shift());
}
// 队尾出队
value = this.queueOut.shift()
// 备份到queueBack中的元素还原到queueOut中
sizeBackup = this.queueBackup.length;
while (sizeBackup--) {
this.queueOut.push(this.queueBackup.shift());
}
}
return value;
};
/**
* @return {number}
*/
MyStack.prototype.top = function() {
let topValue = this.pop();
this.queueOut.push(topValue);
return topValue;
};
/**
* @return {boolean}
*/
MyStack.prototype.empty = function() {
return !this.queueOut.length;
};
/**
* Your MyStack object will be instantiated and called as such:
* var obj = new MyStack()
* obj.push(x)
* var param_2 = obj.pop()
* var param_3 = obj.top()
* var param_4 = obj.empty()
*//* 一个队列模拟栈 */
var MyStack = function() {
this.queue = [];
};
/**
* @param {number} x
* @return {void}
*/
MyStack.prototype.push = function(x) {
this.queue.push(x);
};
/**
* @return {number}
*/
MyStack.prototype.pop = function() {
// 模拟出栈,首先将队尾的元素出队后添加到队尾,然后队尾出队
let size = this.queue.length;
if (size) {
size--;
while (size--) {
this.queue.push(this.queue.pop());
}
return this.queue.pop();
} else {
return null;
}
};
/**
* @return {number}
*/
MyStack.prototype.top = function() {
const value = this.pop();
this.queue.push(value);
return value;
};
/**
* @return {boolean}
*/
MyStack.prototype.empty = function() {
return !this.queue.length;
};
/**
* Your MyStack object will be instantiated and called as such:
* var obj = new MyStack()
* obj.push(x)
* var param_2 = obj.pop()
* var param_3 = obj.top()
* var param_4 = obj.empty()
*/20 有效的括号

用栈来解决对称匹配问题
分析不匹配的三种情况,在这三种情况下,出栈入栈的情况
/**
* @param {string} s
* @return {boolean}
*/
var isValid = function(s) {
let stack = [];
for (let i = 0; i < s.length; i++) {
if (s[i] === '(') {
stack.push(')');
} else if (s[i] === '[') {
stack.push(']');
} else if (s[i] === '{') {
stack.push('}');
} else if (stack.length === 0 || s[i] !== stack[stack.length - 1]) {
return false;
} else {
// s[i] === stack.top()
stack.pop();
}
}
if (stack.length !== 0) {
return false;
}
return true;
};1047 删除字符串中的所有相邻重复项

依然是用栈来解决匹配问题
/**
* @param {string} s
* @return {string}
*/
var removeDuplicates = function(s) {
let stack = [];
let char = "";
let result = "";
for (let i = 0; i < s.length; i++) {
char = s[i];
if (stack.length === 0 || char !== stack[stack.length - 1]) {
stack.push(char);
} else {
stack.pop();
}
}
// 栈的逆序就是结果,但是JavaScript用数组模拟栈,数组的顺序就是结果
stack.forEach(item => result += item);
return result;
};150 逆波兰表达式求值

/**
* @param {string[]} tokens
* @return {number}
*/
var evalRPN = function(tokens) {
let stack = [];
let operators = ["+", '-', "*", "/"];
let num1 = num2 = 0;
let result = 0;
for (let i = 0; i < tokens.length; i++) {
if (operators.indexOf(tokens[i]) > -1) {
if (tokens.length === 1) {
return null;
}
num1 = parseInt(stack.pop());
num2 = parseInt(stack.pop());
switch (tokens[i]) {
case "+":
result = num2 + num1;
break;
case "-":
result = num2 - num1;
break;
case "*":
result = num2 * num1;
break;
case "/":
// 这里不能用floor,floor在商为-0的时候得到的值为-1
// Math.trunc()---保留小数点前的数值
result = Math.trunc(num2 / num1);
result = Math.abs(result) === 0 ? 0 : result;
break;
}
stack.push(result);
} else {
if (tokens.length === 1) {
return tokens[i];
}
stack.push(tokens[i]);
}
}
return stack.pop();
};239 滑动窗口最大值

自定义一个单调队列
/**
* @param {number[]} nums
* @param {number} k
* @return {number[]}
*/
function MyQueue() {
this.queue = []
};
// 每次弹出的时候,比较当前要弹出的数值是否等于队首元素的数值,如果相等则弹出。
MyQueue.prototype.pop = function(value) {
if (this.queue.length && value === this.queue[0]) {
this.queue.shift();
}
}
// 如果push的数值大于队尾元素的数值,那么就将队尾的数值弹出,直到push的数值小于等于队尾元素的数值为止。
MyQueue.prototype.push = function(value) {
while (this.queue.length && value > this.queue[this.queue.length - 1]) {
this.queue.pop();
}
this.queue.push(value);
}
// 返回队首元素的值---窗口中的最大值
MyQueue.prototype.front = function() {
return this.queue[0];
}
var maxSlidingWindow = function(nums, k) {
let myQueue = new MyQueue();
let result = [];
for (let i = 0; i < k; i++) {
myQueue.push(nums[i]);
}
result.push(myQueue.front());
for (let i = k; i < nums.length; i++) {
myQueue.pop(nums[i - k]);
myQueue.push(nums[i]);
result.push(myQueue.front());
}
return result;
};总结
字符串
- 344 反转字符串
- 541 反转字符串 II
344 反转字符串

/**
* @param {character[]} s
* @return {void} Do not return anything, modify s in-place instead.
*/
/* 双指针法 */
// 注意这里输入的是字符数组
var reverseString = function(s) {
let left = 0;
let right = s.length - 1;
while (left < right) {
// 数组解构对变量复制---交换两个变量值的简便写法
[s[left], s[right]] = [s[right], s[left]];
left++;
right--;
}
};541 反转字符串 II

长度k固定,每次移动2k个位置。
不能直接对字符串进行交换字符的操作(无效),应该先将字符串转换成字符数组,对字符数组进行操作。355
/**
* @param {string} s
* @param {number} k
* @return {string}
*/
var reverseStr = function(s, k) {
let left = right = 0;
let result = s.split(""); // 这里先将字符串转换为字符数组
let len = s.length;
// 每次移动2k个字符
for (let i = 0; i < len; i += 2 * k) {
left = i;
// 题目条件
right = i + k > len ? len - 1 : i + k - 1;
while (left < right) {
[result[left], result[right]] = [result[right], result[left]];
left++;
right--;
}
}
return result.join("");
};回溯
77 组合

/**
* @param {number} n
* @param {number} k
* @return {number[][]}
*/
var combine = function(n, k) {
// 递归函数的返回值
let result = new Array();
let path = new Array();
// 1. 定义递归函数,确定参数
function backtracking(n, k, startIndex) {
// 2. 确定递归结束条件
if (path.length === k) {
// JS需要特别注意这里的写法,如果直接将path添加到result中,回溯删除path内元素时会影响result中的值---数组的引用
result.push([...path]);
return ;
}
// 3. for循环横向遍历整个集合,递归子集和
/*
* n - (k - path.length) + 1是剪枝优化
* k-path.length是还需要几个数
* n - (k - path.length) + 1表示至少从哪个数开始是合理的
*/
for (let i = startIndex; i <= n - (k - path.length) + 1 ; i++) {
// 处理结点
path.push(i);
// 递归,控制树的纵向遍历
backTracking(n, k, i + 1);
// 回溯,撤销处理的结点
path.pop();
}
}
backTracking(n, k, 1);
return result;
};216 组合总和 III

- 不能写成result.push(result)—浅拷贝
- 多一个记录path数组和的参数sum
/**
* @param {number} k
* @param {number} n
* @return {number[][]}
*/
var combinationSum3 = function(k, n) {
let result = [];
let path = [];
function backtracking(n, k, sum, startIndex) {
if (path.length === k) {
if (n === sum) {
result.push([...path]);
}
return ;
}
for (let i = startIndex; i <= 9; i++) {
sum += i;
path.push(i);
backtracking(n, k, sum, i + 1);
sum -= i;
path.pop();
}
}
backtracking(n, k, 0, 1);
return result;
};17 电话号码的字母组合

确定递归参数
递归结束条件
细节处理
/**
* @param {string} digits
* @return {string[]}
*/
var letterCombinations = function(digits) {
let num2Letter = [
"", // 0
"", // 1
"abc", // 2
"def", // 3
"ghi", // 4
"jkl", // 5
"mno", // 6
"pqrs", // 7
"tuv", // 8
"wxyz" // 9
];
let result = [];
let path = [];
/**
* index: 处理的第几个数字
*/
function backtracking(digits, index) {
// 当处理的数字个数和给出的digits个数相等时,结束递归
if (digits.length === index) {
result.push(path.join(""));
return;
}
let digit = parseInt(digits[index]);
let letters = num2Letter[digit];
for (let i = 0; i < letters.length; i++) {
path.push(letters[i]);
backtracking(digits, index + 1);
path.pop();
}
}
if (digits === "") {
return result;
} else if (digits.length === 1) {
return num2Letter[parseInt(digits[0])].split("");
}
backtracking(digits, 0);
return result;
};39 组合总和

剪枝优化,写在for循环内部
/**
* @param {number[]} candidates
* @param {number} target
* @return {number[][]}
*/
var combinationSum = function(candidates, target) {
let result = [];
let path = [];
backtracking(candidates, target, 0, 0);
return result;
function backtracking(candidates, target, sum, startIndex) {
if (sum === target) {
result.push([...path]); // 这里要用解构
return ;
}
// 当下一层的sum,即sum+candidates[i] > target就退出本次循环,进入下一次循环
for (let i = startIndex; i < candidates.length; i++) {
// 剪枝优化只能写在这里,不能写在for循环条件判断那里
if (sum + candidates[i] > target) {
continue;
}
path.push(candidates[i]);
sum += candidates[i];
backtracking(candidates, target, sum, i); // 可以选取重复的元素
sum -= candidates[i];
path.pop();
}
}
};40 组合总和II

- 先对数组排序,然后在单层循环里去除重复的组合,没有使用used数组;
- 使用used数组
/**
* @param {number[]} candidates
* @param {number} target
* @return {number[][]}
*/
var combinationSum2 = function(candidates, target) {
let result = [];
let path = [];
candidates = candidates.sort((a, b) => a - b); // 去除重复的组合需要对数组中的数字升序排列
const backtracking = (sum, startIndex) => {
if (sum === target) {
result.push([...path]);
return ;
}
for (let i = startIndex; i < candidates.length; i++) {
// i > startIndex && candidates[i - 1] === candidates[i] 去处重复组合的关键代码
if (sum + candidates[i] > target || (i > startIndex && candidates[i - 1] === candidates[i])) {
continue;
}
sum += candidates[i];
path.push(candidates[i]);
backtracking(sum, i + 1);
sum -= candidates[i];
path.pop();
}
}
backtracking(0, 0);
return result;
};/**
* @param {number[]} candidates
* @param {number} target
* @return {number[][]}
*/
var combinationSum2 = function(candidates, target) {
let result = [];
let path = [];
let used = new Array(candidates.length).fill(false);
candidates = candidates.sort((a, b) => a - b); // 去除重复的组合需要对数组中的数字升序排列
const backtracking = (sum, startIndex) => {
if (sum === target) {
result.push([...path]);
return ;
}
for (let i = startIndex; i < candidates.length; i++) {
// i > 0 && candidates[i - 1] === candidates[i] && used[i - 1] === false 去处重复组合的关键代码
// 树的同一层不能使用相同的元素
if (sum + candidates[i] > target || (i > 0 && candidates[i - 1] === candidates[i] && used[i - 1] === false)) {
continue;
}
sum += candidates[i];
path.push(candidates[i]);
used[i] = true;
backtracking(sum, i + 1);
sum -= candidates[i];
path.pop();
used[i] = false;
}
}
backtracking(0, 0);
return result;
};131 分割回文串

回溯,startIndex就是分割线,子串范围[startIndex, i]
/**
* @param {string} s
* @return {string[][]}
*/
var partition = function(s) {
let result = [];
let path = [];
const backtracking = (startIndex) => {
// startIndex相当于分割线,分割线到字符串的串尾就返回,此时已经分割好结果了
if (startIndex >= s.length) {
result.push([...path]);
return ;
}
for (let i = startIndex; i < s.length; i++) {
// 子串的范围是[startIndex, i]
let str = s.substring(startIndex, i + 1);
if (isPStr(str)) {
path.push(str);
} else {
continue;
}
backtracking(i + 1);
path.pop()
}
}
backtracking(0);
return result;
};
function isPStr(str) {
let left = 0;
let right = str.length - 1;
while (left < right) {
if (str[left] !== str[right]) {
return false;
}
left++;
right--;
}
return true;
}93 复原IP地址

注意:
- 回溯退出的条件
- 单层循环中的逻辑
/**
* @param {string} s
* @return {string[]}
*/
var restoreIpAddresses = function(s) {
let result = [];
let path = [];
const backtracking = (startIndex) => {
if (path.length > 4) {
return ;
}
// path内的4个子串都满足条件,最后用"."拼接
if (path.length === 4 && startIndex === s.length) {
result.push(path.join("."));
return ;
}
for (let i = startIndex; i < s.length; i++) {
// 这里用substring不行,不知道为什么
// substr(satrtIndex, Length) --- 从starIndex开始提取Length个字符
let str = s.substr(startIndex, i - startIndex + 1);
if (str.length > 3 || parseInt(str) > 255) {
// 为什么是直接break?剪枝,不满足条件的可以直接跳过了
break;
}
if (str.length > 1 && str[0] === "0") {
break;
}
path.push(str);
backtracking(i + 1);
path.pop();
}
}
backtracking(0);
return result;
};78 子集

子集,要记录每一个结点的值
/**
* @param {number[]} nums
* @return {number[][]}
*/
var subsets = function(nums) {
let result = [];
let path = [];
const backtracking = startIndex => {
// slice()返回一个新的数组,新数组是由begin和end决定的原数组的浅拷贝
result.push(path.slice()); //记录每一个节点的结果。
// 这里可以不写退出条件,因为当startIndex大于等于集合长度时,本层循环就结束了
if (startIndex >= nums.length) {
return ;
}
for (let i = startIndex; i < nums.length; i++) {
path.push(nums[i]);
backtracking(i + 1);
path.pop();
}
}
backtracking(0);
return result;
};90 子集II

树层去重:
- i > startIndex
- i>0 && used[i - 1] === false
/* i > startIndex */
for (let i = startIndex; i < nums.length; i++) {
if (i > startIndex && nums[i] === nums[i - 1]) {
continue ;
}
path.push(nums[i]);
backtracking(i + 1);
path.pop();
}
/**
* @param {number[]} nums
* @return {number[][]}
*/
var subsetsWithDup = function(nums) {
nums.sort((a, b) => a - b);
let result = [];
let path = [];
let used = new Array(nums.length).fill(false);
const backtracking = startIndex => {
// 子集问题,需要存储每个节点的结果
result.push([...path]);
for (let i = startIndex; i < nums.length; i++) {
// 同一层的上一个结点used[i - 1]为false
if (i > 0 && nums[i] === nums[i - 1] && used[i - 1] === false) {
continue ;
}
used[i] = true;
path.push(nums[i]);
backtracking(i + 1);
path.pop();
used[i] = false;
}
}
backtracking(0);
return result;
};491 递增子序列

/**
* @param {number[]} nums
* @return {number[][]}
*/
var findSubsequences = function(nums) {
let result = [];
let path = [];
const backtracking = startIndex => {
if (path.length >= 2) {
result.push([...path]);
}
let uset = []; // 用数组来做hash映射
for (let i = startIndex; i < nums.length; i++) {
// 如果进入集合下一个元素小于集合的最后一个元素或者nums[i]在同一个父结点下已经使用过了
if ((path.length && nums[i] < path[path.length - 1]) || (uset[nums[i] + 100])) {
continue;
}
uset[nums[i] + 100] = true;
path.push(nums[i]);
backtracking(i + 1);
path.pop();
}
}
backtracking(0);
return result;
};46 全排列

回溯,全排列没有用到startIndex,但是用used数组标记了某个元素是否已经使用。
/**
* @param {number[]} nums
* @return {number[][]}
*/
var permute = function(nums) {
let result = [];
let path = [];
let used = new Array(nums.length).fill(false); // 标记用过的元素
const backtracking = () => {
if (path.length === nums.length) {
result.push([...path]);
return ;
}
for (let i = 0; i < nums.length; i++) {
if (used[i] === true) {
continue ;
}
used[i] = true;
path.push(nums[i]);
backtracking();
used[i] = false;
path.pop();
}
}
backtracking();
return result;
};47 全排列II

排列去重—树层去重与树枝去重都可以,但树层去重效率更高(当数组中的元素重复元素较多时)。
/**
* @param {number[]} nums
* @return {number[][]}
*/
var permuteUnique = function(nums) {
let result = [];
let path = [];
let used = new Array(nums.length).fill(false);
nums.sort((a, b) => a - b);
const backtracking = () => {
if (path.length === nums.length) {
result.push([...path]);
return ;
}
for (let i = 0; i < nums.length; i++) {
// 同一树层去重-->((i > 0 && nums[i - 1] === nums[i]) && used[i - 1] === false)
// used[i]===true --> 全排列
if (((i > 0 && nums[i - 1] === nums[i]) && used[i - 1] === false) || used[i] === true) {
continue ;
}
used[i] = true;
path.push(nums[i]);
backtracking();
used[i] = false;
path.pop();
}
}
backtracking();
return result;
};
for (let i = 0; i < nums.length; i++) {
// 同一树枝去重-->((i > 0 && nums[i - 1] === nums[i]) && used[i - 1] === true)
// used[i]===true --> 全排列
if (((i > 0 && nums[i - 1] === nums[i]) && used[i - 1] === true) || used[i] === true) {
continue ;
}
used[i] = true;
path.push(nums[i]);
backtracking();
used[i] = false;
path.pop();
}贪心
455 分发饼干

贪心思路,先将两个数组升序排序,然后每次将最大的饼干优先分给胃口最大的孩子。
一个for循环就可以了。
/**
* @param {number[]} g
* @param {number[]} s
* @return {number}
*/
var findContentChildren = function(g, s) {
let count = 0;
let sIndex = s.length - 1;
g.sort((a, b) => a - b);
s.sort((a, b) => a - b);
for (let i = g.length - 1; i >= 0; i--) {
if (sIndex >= 0 && s[sIndex] >= g[i]) {
count++;
sIndex--;
}
}
return count;
};376 摆动序列

/**
* @param {number[]} nums
* @return {number}
*/
var wiggleMaxLength = function(nums) {
if (nums.length <= 1) {
return nums.length;
}
let result = 1; // 贪心---局部最优---峰值
let preDiff = 0; // 前一对数字的差
let curDiff = 0; // 当前这对数字的差
for (let i = 0; i < nums.length - 1; i++) {
curDiff = nums[i + 1] - nums[i];
if ((preDiff >= 0 && curDiff < 0) || (preDiff <= 0 && curDiff > 0)) {
result++;
preDiff = curDiff;
}
}
return result;
};53 最大子数组和

- 暴力两个for循环
- 贪心思想的解法,将时间复杂度降低了一个数量级
/* 暴力解法 */
/**
* @param {number[]} nums
* @return {number}
*/
var maxSubArray = function(nums) {
if (nums.length === 1) {
return nums[0];
}
let maxSum = Number.MIN_SAFE_INTEGER;
let sum = 0;
for (let i = 0; i < nums.length; i++) {
sum = 0;
for (let j = i; j < nums.length; j++) {
sum += nums[j];
maxSum = sum > maxSum ? sum : maxSum;
}
}
return maxSum;
};
/* 贪心思路 */
/** 贪心思路的解法
* @param {number[]} nums
* @return {number}
*/
var maxSubArray = function(nums) {
if (nums.length === 1) {
return nums[0];
}
let maxSum = Number.MIN_SAFE_INTEGER; // 设置最值
let sum = 0; // 循环迭代的值
for (let i = 0; i < nums.length; i++) {
sum += nums[i];
// 确定最大和序列的终点
if (sum > maxSum) {
maxSum = sum;
}
// 确定最大和序列的起点---sum<=0说明nums[i]是负数,从下一个元素开始找最大和
if (sum <= 0) {
sum = 0;
}
}
return maxSum;
};总结
动态规划
DP(Dynamic programming): 动态规划
五部曲:
- 确定dp数组及下标含义;
- 确定递推公式;
- 初始化dp数组
- 确定dp数组的遍历方向;
- 举例